8. Sistemas de Referência de Coordenadas

	Objetivos:	Compreendendo os Sistemas de Referência de Coordenadas
	Palavras-chave:	Sistemas de Referência das Coordenadas (SRC), Projeção do Mapa, Projeção em Tempo Real, Latitude, Longitude, Coordenada Norte, e Coordenada Leste

8.1. Visão Global

Projeções cartográficas tentam retratar a superfície da terra, ou uma porção da terra, num pedaço plano de papel ou em uma tela de computador. Em termos leigos, projeções cartográficas tentam transformar a terra de sua forma esférica (3D) para uma forma plana (2D).

Um sistema de referência de coordenadas (SRC) define como o mapa bidimensional projetado em seu SIG se relaciona com lugares reais na Terra. A decisão de qual projeção de mapa e SRC usar depende da extensão regional da área em que você deseja trabalhar, da análise que deseja fazer e, geralmente, da disponibilidade de dados.

8.2. Projeção Cartográfica em detalhe

Um método tradicional de representar a forma da terra é usar globos. Há, no entanto, um problema com esta abordagem. Embora globos preservem a maioria da forma da terra e ilustrem a configuração espacial de elementos de dimensão continental, são difíceis de carregar num bolso. São também apenas convenientes de usar em escalas extremamente pequenas (p. ex. 1:100 milhões).

A maioria dos dados de mapas temáticos utilizados em aplicações SIG têm uma escala consideravelmente maior. Conjuntos de dados SIG típicos têm escalas de 1:250.000 ou maiores, dependendo do nível de detalhe. Uma globo com este tamanho seria difícil e dispendioso de produzir e ainda mais difícil de transportar. Consequentemente, os cartógrafos desenvolveram um conjunto de técnicas designadas por projeções cartográficas concebidas para representar, com precisão razoável, a terra esférica em duas dimensões.

Quando observada de perto a terra aparenta ser relativamente plana. Contudo quando a observamos do espaço, podemos ver que a terra é relativamente esférica. Mapas, como aqueles que veremos posteriormente no tópico dedicado à produção de mapas, são representações da realidade. São concebidos não apenas para representar entidades, mas também a sua forma e disposição espacial. Qualquer projeção cartográfica tem vantagens e desvantagens. A melhor projeção para um mapa depende da escala do mapa, e dos objetivos para os quais será usado. Por exemplo, uma projeção poderá ter distorções inaceitáveis se usada num mapa de todo o continente Africano, mas poderá ser uma excelente escolha para um mapa numa escala grande (detalhado) do seu país. As propriedades de uma projeção cartográfica podem também influenciar algumas características na concepção do mapa. Algumas projeções são indicadas para pequenas áreas, outras são indicadas para representar áreas com uma grande extensão Este-Oeste, e outras são mais apropriadas para representar áreas com uma grande extensão Norte-Sul.

8.3. As três famílias das projeções cartográficas

O processo de criação de projeções de mapas é melhor ilustrado posicionando uma fonte de luz dentro de um globo transparente no qual são colocadas características opacas da terra. Em seguida, projete os contornos da feição em um pedaço de papel plano bidimensional. Diferentes maneiras de projetar podem ser produzidas cercando o globo de maneira cilíndrica, como um cone ou mesmo como uma superfície plana. Cada um desses métodos produz o que é chamado de família de projeção de mapas. Portanto, há uma família de projeções planas, uma família de projeções cilíndricas e outra chamada projeções cônicas (veja figure_projection_families)

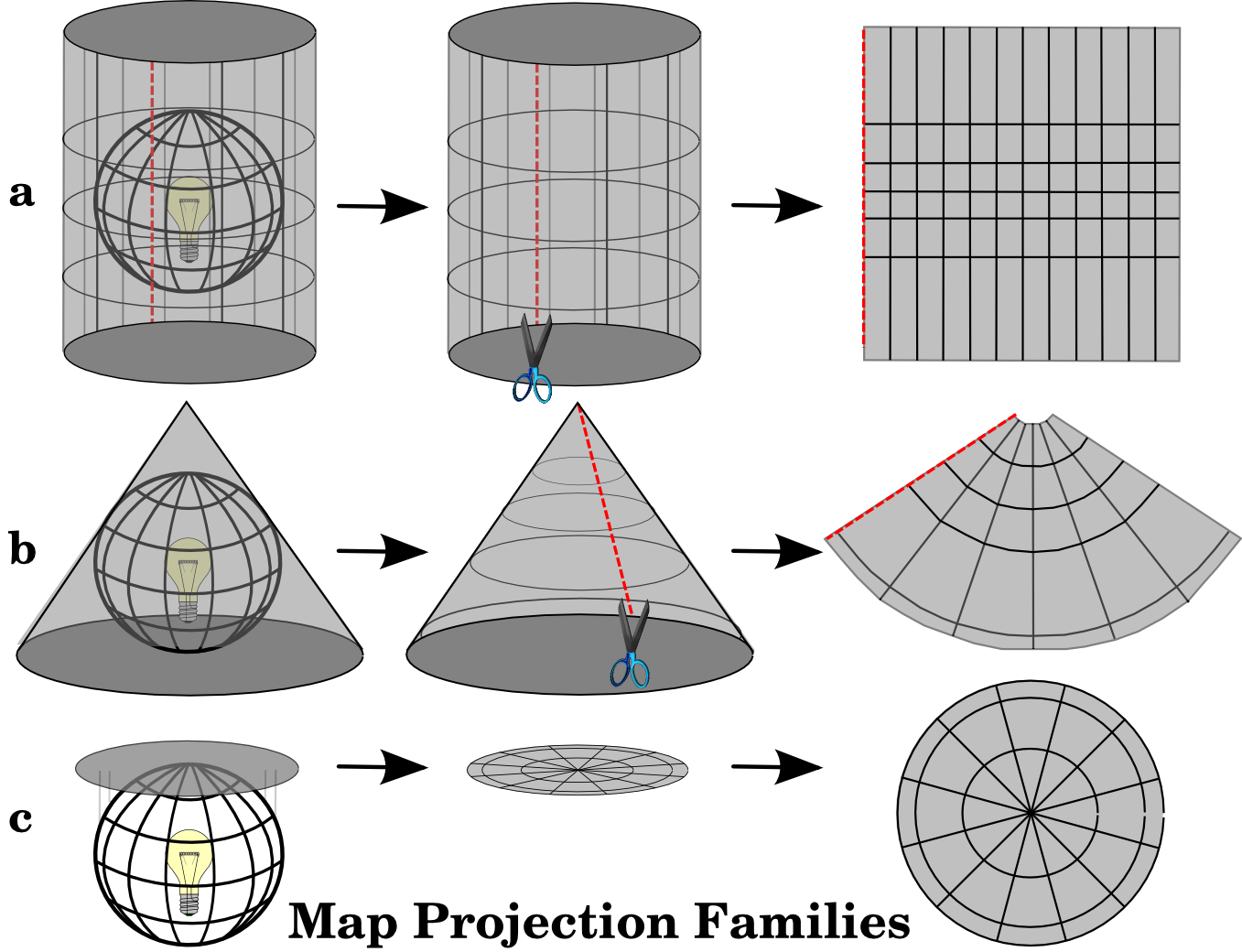
Fig. 8.3 Os três tipos de projeções cartográficas. Podem ser representadas por a) projeções cilíndricas, b) projeções cônicas ou c) projeções planares.

Hoje, naturalmente, o processo de projetar uma terra esférica num papel plano é feito usando princípios matemáticos de geometria e trigonometria, reproduzindo-se a projeção física de luz através do globo.

8.4. Precisão das projeções cartográficas

Projeções de mapas nunca são representações absolutamente precisas da Terra esférica. Como resultado do processo de projeção do mapa, todo mapa mostra distorções da conformidade angular, distância e área. Uma projeção de mapa pode combinar várias dessas características, ou pode distorcer todas as propriedades de área, distância e conformidade angular, dentro de um limite aceitável. Exemplos de projeções de comprometimento são a projeção Winkel Tripel e a projeção Robinson (veja a figure_robinson_projection), que são frequentemente usadas para produzir e visualizar mapas do mundo.

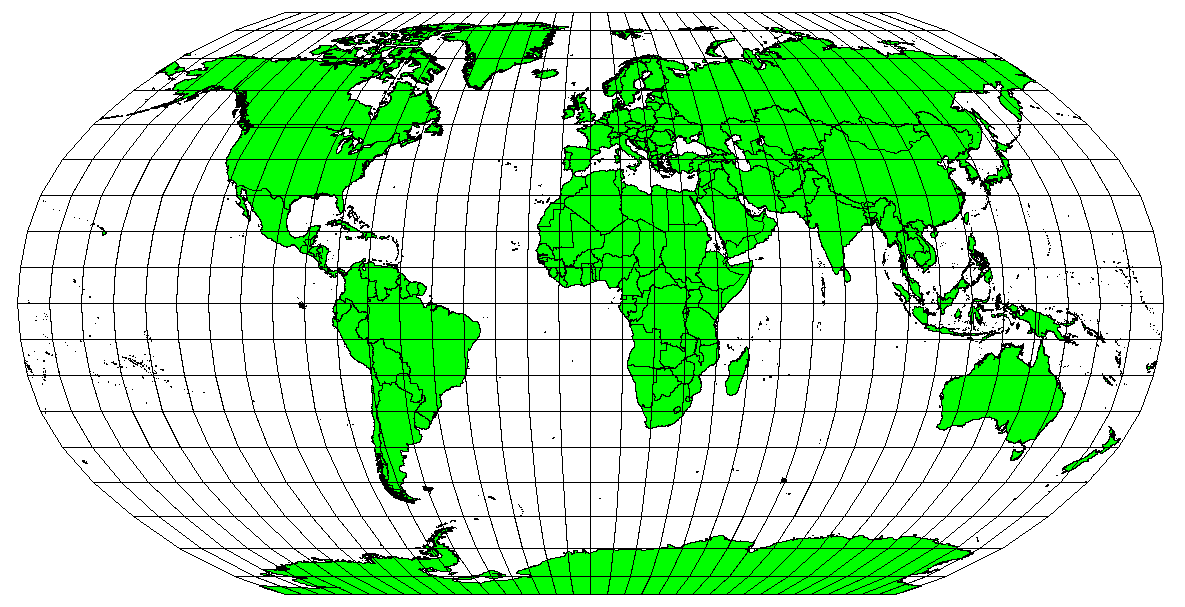
Fig. 8.4 A projeção de Robinson é um compromisso entre distorções de área, ângulo e direção, e distância que são aceitáveis.

É geralmente impossível preservar todas as características em simultâneo numa projeção cartográfica. Isto significa que quando queremos executar operações analíticas precisas necessitamos de usar uma projeção cartográfica que fornece as melhores características para as nossas análises. Por exemplo, se for necessário medir distâncias no nosso mapa, devemos usar uma projeção que garante uma elevada precisão nas distâncias.

8.4.1. Projeções cartográficas com conformidade angular

Ao trabalhar com um globo, as principais direcções da rosa dos ventos (Norte, Este, Sul e Oeste) ocorrerão sempre a 90º umas das outras. Por outras palavras, Este ocorrerá sempre num ângulo de 90º com a direcção Norte. As propriedades angulares corretas podem ser preservadas numa projeção. Uma projeção que mantém ângulos e direções é designada de projeção conforme ou projeção ortomórfica.

Estas projeções são usadas quando a preservação das relações angulares é importante. São usadas geralmente para tarefas de navegação ou meteorologia. É importante relembrar que manter verdadeiros os ângulos num mapa é difícil para grandes áreas e deve ser apenas tentado para pequenas porções da terra. O tipo de projeções Conformes resulta em distorções de áreas, o que significa que se forem efetuadas medições de área no mapa, estas serão incorretas. Quanto maior a área menos precisas serão as medições de área. Exemplos são a projeção de Mercator (como ilustrado na figure_mercator_projection) e a projeção Cônica Conforme de Lambert. O U.S. Geological Survey usa uma projeção conforme para muitos dos seus mapas topográficos.

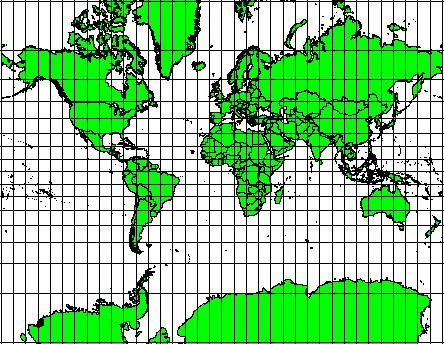
Fig. 8.5 A projeção de Mercator, por exemplo, é usada quando relações angulares são importantes, mas as relações entre áreas são distorcidas.

8.4.2. Projeções cartográficas com distâncias equivalentes

Se o seu objetivo ao projetar um mapa é medir distâncias com precisão, deve selecionar uma projeção que é concebida para preservar distâncias corretamente. Estas projeções, designadas projeções equidistantes, necessitam que a escala do mapa seja mantida constante. Um mapa é equidistante quando representa distâncias corretamente a partir do centro de projeção até qualquer outro local no mapa. Projeções Equidistantes mantêm distâncias precisas a partir do centro de projeção ou ao longo de certas linhas. Estas projeções são usadas para mapas de rádio ou sismologia, e para navegação. A Projeção Cilíndrica Equidistante de Plate Carree (ver figure_plate_caree_projection) e a projeção Equiretangular são dois bons exemplos de projeções equidistantes. A **projeção Equidistante Azimutal ** é a projeção usada no emblema das Nações Unidas (ver figure_azimuthal_equidistant_projection).

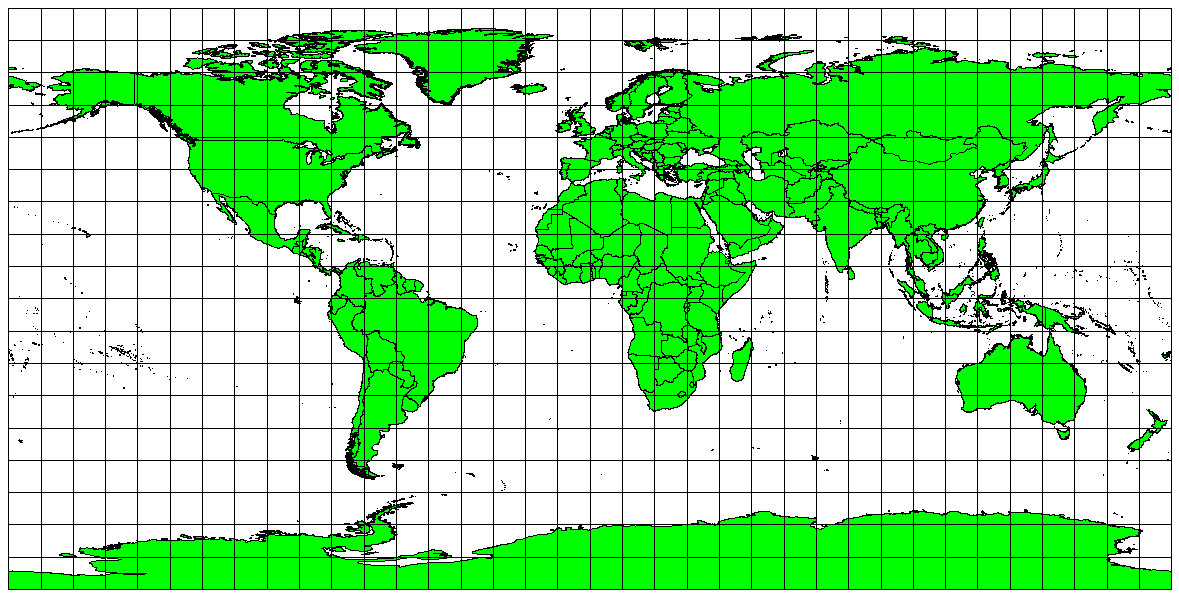
Fig. 8.6 A projeção Cilíndrica Equidistante de Plate Carree, por exemplo, é usada quando a medição precisa de distâncias é importante.

Fig. 8.7 O Logo das Nações Unidas usa a projeção Equidistante Azimutal.

8.4.3. Projeções com áreas equivalentes

Quando um mapa retrata áreas em todo o mapa, de modo que todas as áreas mapeadas tenham a mesma relação proporcional às áreas na Terra que representam, o mapa é um mapa de área igual. Na prática, os mapas educacionais e de referência geral geralmente requerem o uso de projeções de áreas iguais. Como o nome indica, esses mapas são melhor utilizados quando os cálculos de área são os principais cálculos que você executará. Se, por exemplo, você está tentando analisar uma área específica da sua cidade para descobrir se ela é grande o suficiente para um novo shopping, projeções de áreas iguais são a melhor opção. Por um lado, quanto maior a área que você está analisando, mais precisas serão as medidas de sua área, se você usar uma projeção de área igual em vez de outro tipo. Por outro lado, uma projeção de área igual resulta em distorções da conformidade angular ao lidar com grandes áreas. Áreas pequenas serão muito menos propensas a distorcer seus ângulos quando você usar uma projeção de área igual. Área igual de Alber, Área igual de Lambert e Projeções cilíndricas de área igual a Mollweide (mostradas na figure_mollweide_equal_area_projection) são tipos de projeções de área igual que são frequentemente encontradas no trabalho SIG.

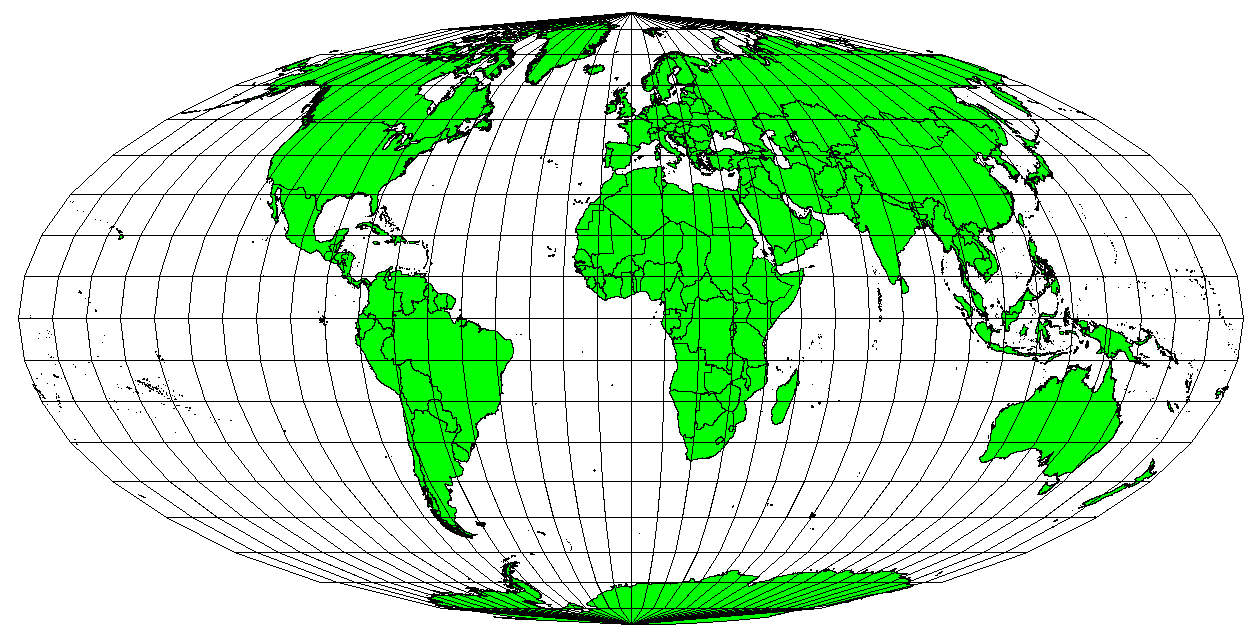
Fig. 8.8 A projeção Cilíndrica Equivalente de Mollweide, por exemplo, garante que todas as áreas cartografas têm a mesma relação proporcional com as áreas na Terra.

Tenha em atenção que as projeções cartográficas são um tópico muito complexo. Existem centenas de diferentes projeções disponíveis em todo o mundo, cada tentando retratar uma certa porção da superfície da terra o mais fielmente possível num pedaço plano de papel. Na realidade, a escolha de qual a projeção a usar será frequentemente estará já tomada. A maioria dos países têm as suas projeções mais comuns e quando informação é trocada, em geral segue-se a norma nacional.

8.5. Sistemas de Referência de Coordenadas (SRC) em detalhe

Com a ajuda dos sistemas de referência de coordenadas (SRC) cada lugar na terra pode ser especificado por um conjunto de 3 números, chamados coordenadas. Em geral, os SRC podem ser divididos ente sistemas de coordenadas projetados (também designados por sistemas de coordenadas Cartesianas ou retangulares) e sistemas de coordenadas geográficas.

8.5.1. Sistemas de Coordenadas Geográficas

O uso de Sistemas de Coordenadas Geográficas é muito comum. Estes usam graus de latitude e longitude e por vezes um valor de altura para descrever uma localização na superfície da terra. O mais popular é chamado WGS 84.

Linhas de latitude são paralelas ao equador e dividem a terra em 180 seções igualmente espaçadas entre si deste o Norte ao Sul (ou do Sul ao Norte). A linha de referência para a latitude é o equador e cada hemisfério é dividido em noventa seções, cada representando um grau de latitude. No hemisfério norte, os graus de latitude são medidos de 0 no equador até 90 graus no pólo norte. No hemisfério sul, os graus de latitude são medidos de 0 no equador até 90 graus no pólo sul. Para simplificar a digitação de mapas, os graus de latitude no hemisfério sul são muitas vezes representados como valores negativos (0 a -90º). Sempre que esteja na superfície da terra, a distância entre linhas de latitude é a mesma (60 milhas náuticas). Ver figure_geographic_crs para uma ilustração.

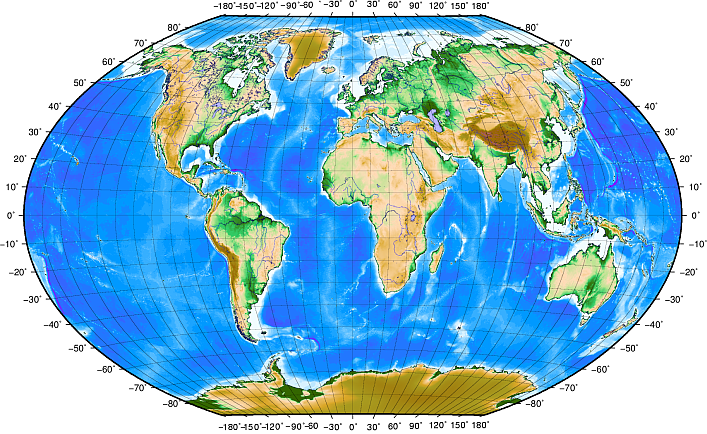
Fig. 8.9 Sistemas de coordenadas geográficas com linhas de latitude paralelas ao equador e linhas de longitude com o meridiano principal a passando por Greenwich.

Linhas de longitude, por outro lado, não são tão uniformes. Linhas de longitude são perpendiculares ao equador e convergem nos pólos. A linha de referência para a longitude (o meridiano principal) desenvolve-se a partir do pólo Norte até ao pólo Sul passando por Greenwich, Inglaterra. Linhas de longitude subsequentes são medidas de 0 a 180 graus Este ou Oeste em relação ao meridiano principal. Note que os valores a Oeste do meridiano principal são negativos para uso em aplicações de cartografia digital. Ver figure_geographic_crs para uma ilustração.

No equador, e apenas no equador, a distância representada por uma linha de longitude é igual à distância representada por um grau de latitude. Ao mover-se para os pólos, a distância entre linhas de longitude torna-se progressivamente menor, até que, na exata localização do pólo, todos os 360º de longitude são representados por um único ponto que pode tocar com o seu dedo (quererá provavelmente usar luvas). Usando o sistema de coordenadas geográfico, podemos ter uma grade de linhas dividindo a terra em quadrados que cobrem aproximadamente 12363,365 quilômetros quadrados até ao equador — um bom início, mas não muito útil para determinar a localização de algo num desses quadrados.

Para ser realmente útil, uma grade no mapa deve ser dividida em seções suficientemente pequenas para que possam ser usadas para descrever (com um nível de precisão aceitável) a localização de um ponto no mapa. Para isto, graus são divididos em minutos (') e segundos ("). Existem sessenta minutos num grau, e sessenta segundos num minuto (3600 segundos num grau). Assim, no equador, um segundo de latitude ou longitude = 30,87634 metros.

8.5.2. Sistemas de coordenadas projetadas

Um sistema bidimensional de coordenadas é frequentemente definido por dois eixos. Em ângulos retos entre si, formam o denominado plano XY (ver figure_projected_crs à esquerda). O eixo horizontal é normalmente marcado com X, e o eixo vertical é normalmente assinalado com Y. Num sistema tridimensional de coordenadas, outro eixo, normalmente designado por Z, é adicionado. É também posicionado em ângulos retos em relação aos eixos X e Y. O eixo Z fornece a terceira dimensão do espaço (ver figure_projected_crs à direita). Cada ponto que é expresso em coordenadas esféricas pode ser expresso como uma coordenada X Y Z.

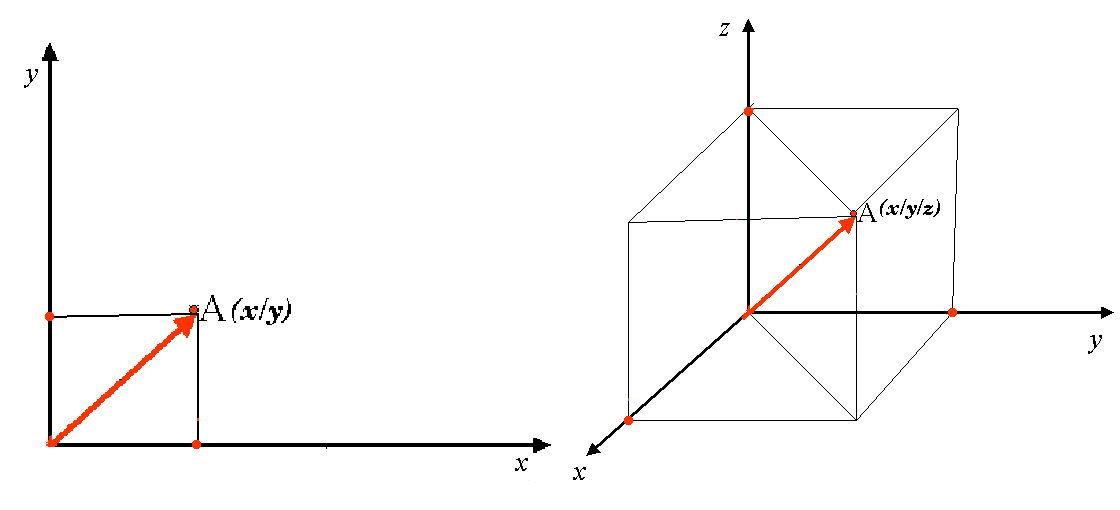
Fig. 8.10 Sistemas de coordenadas de duas e três dimensões

Um sistema de coordenadas projetadas no hemisfério sul (a sul do equador) normalmente tem a sua origem no equador numa Longitude específica. Isto significa que os valores de Y aumentam para Sul e os valores de X aumentam para Oeste. No hemisfério norte (a norte do equador) a origem é também o equador numa Longitude específica. Contudo, agora os valores de Y aumentam para Norte e os valores de X aumentam para Este. Na seção seguinte, descreveremos um sistema de coordenadas projetadas, chamado Universal Transverso de Mercator (UTM) muito usado para a África do Sul.

8.6. O SRC Universal Transverso de Mercator (UTM) em detalhe

O sistema de referência de coordenadas Universal Transverse Mercator (UTM) tem sua origem no equador em uma Longitude específica. Agora, os valores Y aumentam para o sul e os valores X aumentam para o oeste. O UTM SRC é uma projeção de mapa global. Isso significa que geralmente é usado em todo o mundo. Mas, como já descrito na seção ‘precisão das projeções de mapas’ acima, quanto maior a área (por exemplo, África do Sul), mais distorções de conformidade angular, distância e área ocorrem. Para evitar muita distorção, o mundo é dividido em 60 zonas iguais, todas com 6 graus de largura, de leste a oeste. As zonas UTM são numeradas 1 a 60, começando no antimeridiano (zona 1 a 180 graus de longitude oeste) e avançando para o leste de volta ao antimeridiano ( zona 60 a 180 graus de longitude leste), como mostra a figure_utm_zones.

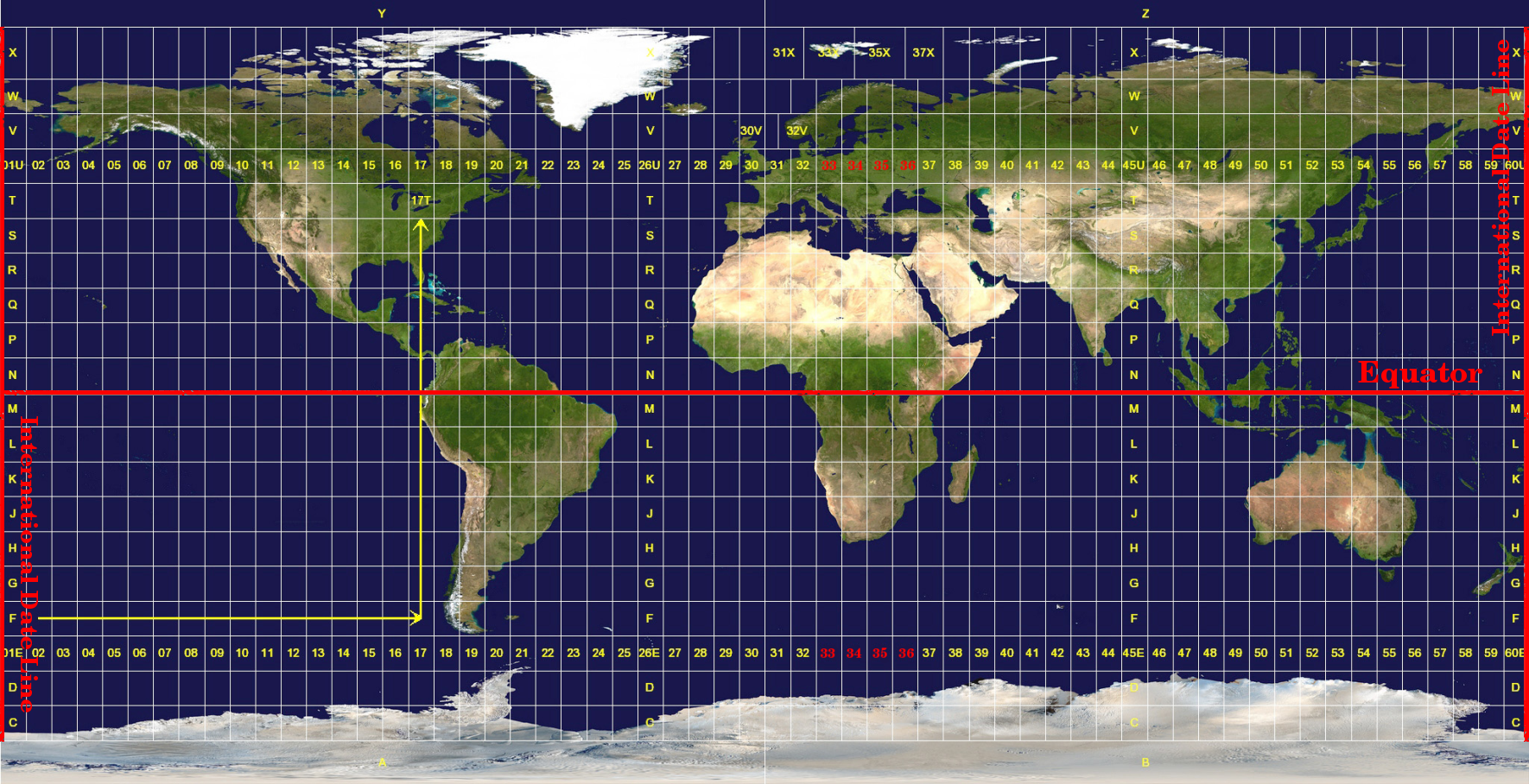
Fig. 8.11 As zonas do sistema Universal Transverso de Mercator. Para a África do Sul são usadas as zonas 33S, 34S, 35S, e 36S.

Como pode ver nas figure_utm_zones e figure_utm_for_sa, a África do Sul é coberta por quatro zonas UTM para minimizar distorções. As zonas são chamadas UTM 33S, UTM 34S, UTM 35S e UTM 36S. O S após a zona significa que as zonas UTM estão localizadas a sul do equador.

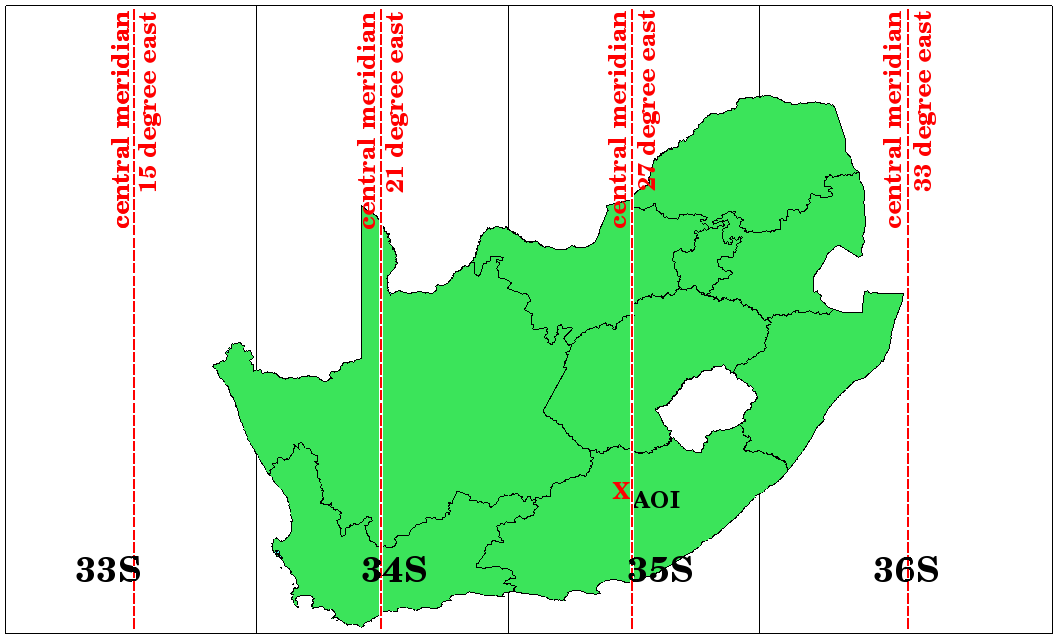
Fig. 8.12 Zonas UTM 33S, 34S, 35S, e 36S com as suas longitudes centrais (meridianos) usadas para projetar a África do Sul com alta precisão. A cruz vermelha mostra uma Área de Interesse (ADI).

Imagine, por exemplo, que queremos definir um sistema de coordenadas bidimensional dentro da Área de Interesse (ADI) marcada com uma cruz vermelha na figure_utm_for_sa. Pode ver que a área está localizada dentro da zona UTM 35S. Isto significa que, para minimizar a distorção e obter resultados de análise precisos, devemos usar a zona UTM 35S como o sistema de referência de coordenadas.

A posição de uma coordenada em UTM ao sul do equador deve ser indicada com o número da zona (35) e com seu valor norte (Y) e valor leste (X), em metros. O valor norte é a distância da posição do equador, em metros. O valor leste é a distância do meridiano central (longitude) da zona UTM usada. Para a zona UTM 35S, são 27 graus Leste, como mostrado na figure_utm_para_sa. Além disso, como estamos ao sul do equador e os valores negativos não são permitidos no sistema de referência de coordenadas UTM, temos que adicionar um chamado falso valor norte” de 10.000.000 m ao valor norte (Y) e um falso leste 500.000 m para o valor leste (X). Como Isso pode parecer difícil, faremos um exemplo que mostra como encontrar a coordenada **UTM 35S correta para a Área de interesse.

8.6.1. O valor norte (Y)

O local que procuramos é de 3.550.000 metros ao sul do equador, então o valor do norte (Y) recebe um sinal negativo e é -3.550.000 m. De acordo com as definições da UTM, precisamos adicionar um falso valor norte de 10.000.000 m. Isso significa que o valor norte (Y) de nossa coordenada é 6.450.000 m (-3.550.000 m + 10.000.000 m).

8.6.2. O valor leste (X)

Primeiramente, temos que encontrar o meridiano central (longitude) para a zona UTM 35S. Como podemos ver na figure_utm_para_sa, é 27 graus leste. O local que procuramos está a 85.000 metros a oeste do meridiano central. Assim como o valor do norte, o valor do leste (X) recebe um sinal negativo, resultando em - 85.000 m. De acordo com as definições da UTM, temos de adicionar um falso valor leste de 500.000 m. Isso significa que o valor leste (X) de nossa coordenada é 415.000 m (-85.000 m + 500.000 m). Finalmente, temos que adicionar o número da zona ao valor leste para obter o valor correto.

Como resultado, a coordenada para o nosso Ponto de Interesse, projetado na zona UTM 35S seria escrito como: 35 415.000 m E / 6.450.000 m N. Em alguns SIG, quando a zona UTM 35S é definida com a correta e as unidades escolhidas são metros, as coordenadas podem aparecer como simplesmente 415.000 6.450.000.

8.7. Projeção em Voo-livre

Como pode provavelmente imaginar, pode surgir uma situação onde os dados que quer usar num SIG estão projetados num sistema de coordenadas diferente. Por exemplo, poderá ter um tema vetorial com os limites da África do Sul projetados em UTM 35S e outro tema vectorial de pontos com informação sobre precipitação fornecido no sistema de coordenadas geográficas WGS 84. Num SIG estes dois temas vetoriais são mostrados em duas áreas totalmente diferentes na janela do mapa, porque têm diferentes projeções.

Para resolver esse problema, muitos SIG incluem uma funcionalidade chamada projeção on-the-fly. Isso significa que você pode definir uma certa projeção ao iniciar o SIG e todas as camadas que você carrega, independentemente do sistema de referência de coordenadas que eles possuem, serão exibidas automaticamente na projeção que você definiu. Essa funcionalidade permite sobrepor camadas na janela de mapa do seu SIG, mesmo que elas estejam em diferentes sistemas de referência. No QGIS, essa funcionalidade é aplicada por padrão.

8.8. Problemas comuns / situações a que deve estar atento

O tópico projeções do mapa é muito complexo e até profissionais que estudaram geografia, geodésica ou outra ciência relacionada com SIG, muitas vezes têm problemas com a definição correta de projeções cartográficas e sistemas de referência de coordenadas. Geralmente quando se trabalha com SIG, já temos dados para começar a trabalhar. Na maioria das vezes, estes dados estarão projetados num determinado SRC, e não terá de criar o novo SRC nem mesmo de re-projetar os dados de um SRC para outro. Dito isto, é sempre útil ter uma noção do que significam projeção cartográfica e SRC.

8.9. O que aprendemos?

Resumindo o que abordamos na lista seguinte:

• Projeções do mapa representam a superfície da terra num pedação de papel, ou tela de computador, bidimensional.

• Existem projeções cartográficas globais, mas a maioria das projeções são criadas e optimizadas para áreas menores da superfície da terra.

• Projeções cartográficas nunca são representações totalmente precisas da terra esférica. Mostram distorções da conformidade angular, de distâncias e de áreas. É impossível preservar todas estas características ao mesmo tempo numa projeção cartográfica.

• UM Sistema de referência de coordenadas (SRC) define, com a ajuda de coordenadas, como o mapa bidimensional projetado se relaciona com locais reais na terra.

• Há dois tipos diferentes de sistemas de referência de coordenadas: Sistemas de Coordenadas Geográficas e Sistemas de Coordenadas Projetadas.

• A projeção Em Voo livre é uma funcionalidade em SIG que nos permite sobrepor camadas, ainda que estejam projetadas em diferentes sistemas de referencia de coordenadas.

8.10. Agora vamos tentar!

Aqui estão algumas idéias para tentar com seus alunos:

1. Inicie o QGIS

2. Em Projeto ▶ Propriedades… ▶ SRC verifique :guilabel:`Nenhuma projeção (ou projeção desconhecida/não terrestre)

3. Carregue duas camadas da mesma área, mas com projeções diferentes

4. Let your pupils find the coordinates of several places on the two layers. You can show them that it is not possible to overlay the two layers.

5. Em seguida, defina o sistema de referência de coordenadas como Geographic/WGS 84 dentro da caixa de diálogo: guilabel: Project Properties

6. Load the two layers of the same area again and let your pupils see how setting a CRS for the project (hence, enabling “on-the-fly” projection) works.

7. Você pode abrir a caixa de diálogo: guilabel: Propriedades do projeto no QGIS e mostrar a seus alunos os diferentes Sistemas de Referência de Coordenadas para que eles tenham uma idéia da complexidade deste tópico. Você pode selecionar diferentes CRSs para exibir a mesma camada em diferentes projeções.

8.11. Algo para refletir

Se você não tiver um computador disponível, pode mostrar aos alunos os princípios das três famílias de projeção de mapas. Usando um globo e papel, demonstre como as projeções cilíndricas, cônicas e planas funcionam em geral. Com a ajuda de uma folha de transparência, você pode desenhar um sistema de referência de coordenadas bidimensional mostrando os eixos X e Y. Em seguida, deixe seus alunos definirem coordenadas (valores X e Y) para diferentes lugares.

8.12. Leituras adicionais

Livros:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986

• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195

• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

Páginas Web:

• https://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html

• https://geology.isu.edu/wapi/geostac/Field_Exercise/topomaps/index.htm

A Guia do Usuário QGIS também tem mais informação detalhada acerca de como trabalhar com projeções cartográficas em QGIS.

8.13. O que segue?

Na seção que segue vamos ver mais de perto a Produção do Mapa.