Topologia¶

Vedere generală¶

Topologia exprimă relațiile spațiale dintre entitățile vectoriale conectate sau adiacente (puncte, polilinii și poligoane) dintr-un GIS. Datele topologice, sau pe bază de topologie, sunt utile pentru detectarea și corectarea erorilor de digitizare (de exemplu, două linii dintr-un strat de drumuri vectoriale care nu se întâlnesc perfect la o intersecție). Topologia este necesară pentru realizarea unor genuri de analize spațiale, cum ar fi analiza de rețea.

Imaginați-vă că vă deplasați spre Londra. Cu ajutorul unei hărți turistice vă planificați mai întâi o vizită la Catedrala Sf Paul, urmată de alta la Covent Garden Market, pentru unele suveniruri. Privind pe harta metroului londonez (a se vedea figure_topology_london) va trebui să identificați trenurile de legătură dintre Covent Garden și Sf. Paul. Acest lucru necesită informații topologice (date) cu privire la posibilitatea de schimbare a trenurilor. Privind la o hartă a metroului, relațiile topologice sunt ilustrate prin cercuri care arată conexiunile.

Topologia rețelei de metrou din Londra

Erori de topologie¶

Există diferite tipuri de erori topologice, ele putând fi grupate în funcție de caracterul de poligon sau polilinie al entităților vectoriale. Printre erorile topologice, în cazul entităților de tip poligon, se pot include poligoanele nefinalizate, breșele sau suprapunerile limitelor poligoanelor. O eroare topologică obișnuită, în cazul entităților de tip polilinie, o reprezintă faptul că acestea nu sunt tangente la un punct (nod). Acest tip de eroare poartă numele neîncadrare dacă există o breșă între linii, sau depășire dacă o linie se termină dincolo de linia la care ar trebui să se conecteze (a se vedea figure_topology_errors).

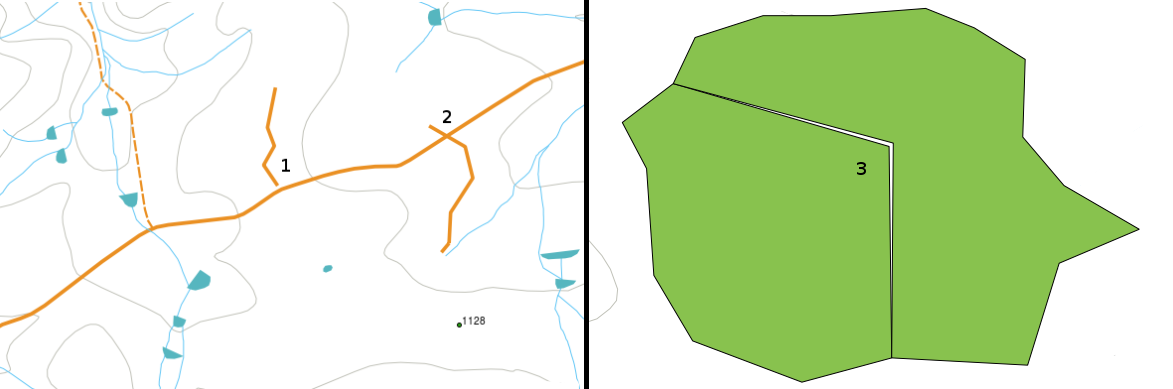
Erorile de neîncadrare (1) apar atunci când liniile vectoriale digitizate, care ar trebuie să fie conectate între ele, nu se ating. Depășirile (2) apar atunci când o linie se termină dincolo de linia la care ar trebui să se conecteze. Așchiile (3) apar atunci când vârfurile a două poligoane nu aderă perfect la laturile lor.

Rezultatul erorilor de neîncadrare și de depășire sunt așa-numitele ‘noduri incerte’ de la capătul liniilor. Nodurile incerte sunt acceptabile în cazuri speciale, cum ar fi cazul în care sunt atașate unor străzi care se înfundă.

Erorile topologice denaturează relațiile dintre entități. Aceste erori trebuie să fie reparate, pentru a fi în măsură să studiați datele vectoriale cu proceduri cum ar fi analiza de rețea (de exemplu, găsirea cel mai bun traseu într-o rețea de drumuri) sau prin măsurători (de exemplu, aflarea lungimii unui râu). În plus, există și alte motive pentru care este important și util să creați sau să aveți date vectoriale cu topologie corectă. Doar imaginați-vă că digitizați o hartă a granițelor municipale pentru provincia dvs., și că poligoanele se suprapun sau prezintă așchii. Dacă există astfel de erori, deși veți putea utiliza instrumentele de măsurare, rezultatele pe care le obține vor fi incorecte. Nu veți cunoaște suprafața corectă și nici nu veți fi în măsură să precizați cu exactitate unde sunt granițele dintre municipalități.

Nu este important doar pentru propria analiză să creați și să aveți date corecte din punct de vedere topologic, ci și pentru cei cărora le transmiteți datele. Aceștia se așteaptă ca datele și rezultatele analizei să fie corecte!

Reguli topologice¶

Din fericire, multe din erorile care pot apărea la digitizarea entităților vectoriale pot fi prevenite prin regulile de topologie care sunt implementate în multe aplicații GIS.

Cu excepția unor formate de date GIS speciale, topologia nu este, de obicei activată în mod implicit. Multe aplicații GIS comune, cum ar fi QGIS, definesc topologia sub formă de reguli relaționate, permițând utilizatorului să aleagă regulile care vor fi implementate într-un strat vectorial.

Lista de mai jos prezintă câteva exemple în care regulile topologie pot fi definite pentru entități ale lumii reale într-o hartă vectorială:

• Marginile hărții unei municipalități nu trebuie să se suprapună.

• Marginile unei hărți pentru o municipalitate nu trebuie să aibă lacune (șuvițe).

• Poligoanele care indică limitele de proprietate trebuie să fie închise. Depășirile liniilor de frontieră, inclusiv cele negative, nu sunt permise.

• Curbele de nivel dintr-un strat vectorial de tip linie nu trebuie să se intersecteze (nu au voie să se încrucișeze).

Instrumente topologice¶

Multe aplicații GIS oferă instrumente de editare topologică. De exemplu, în QGIS puteți activa editarea topologică pentru a îmbunătăți editarea și pentru menținerea granițelor comune în straturile poligonale. Un GIS cum este QGIS ‘detectează’ o graniță comună într-o hartă poligonală, așa că trebuie doar să mutați vertexul unei limite poligonale, iar QGIS va asigura actualizarea celorlalte limite poligonale, așa cum se arată în figure_topological_tools (1).

O altă opțiune topologică vă permite să împiedicați suprapunerea poligonală pe durata digitizării (a se vedea figure_topological_tools (2)). Dacă aveți deja un poligon, este posibil, cu această opțiune să digitizați un al doilea poligon adiacent, astfel încât ambele poligoane să se suprapună, apoi QGIS va decupa al doilea poligon la limita comună.

(1) Topological editing to detect shared boundaries, when moving vertices. When moving a vertex, all features that share that vertex are updated. (2) To avoid polygon overlaps, when a new polygon is digitised (shown in red) it is clipped to avoid overlapping neighbouring areas.

Distanța de acroșare¶

Distanța de acroșare reprezintă distanța până la care un GIS caută cel mai apropiat vertex și / sau segment la care încearcă să se conecteze, atunci când are loc digitizarea. Un segment este o linie dreaptă formată între două noduri dintr-o geometrie de tip poligon sau polilinie. Dacă distanța de acroșare este depășită, un GIS va lăsa vertexul în locul în care s-a eliberat butonul mouse-ului, în locul acroșării la un nod sau la un segment existent (a se vedea figure_snapping_distance).

Distanța de acroșare (cercul negru) este definită în unități de hartă (de exemplu, în grade zecimale), pentru acroșarea fie la noduri, fie la segmente.

Raza de căutare¶

Cautarea radiala reprezinta distanta pe care un GIS o utilizeaza in cautarea celui mai apropiat vertex cand incercati sa il mutati in momentul in care faceti click pe harta. Daca nu sunteti in cadrul cautarii radiale, GIS-ul nu va gasi si selecta nici un vertex al entitatii selectate. In principiu, este asemanatoare cu functionalitatea distanta saltului.

Distanta saltului si cautarea radiala sunt amandoua setate in unitatile de masura ale hartii deci va trebui sa faceti cateva experimente pentru a afla valoarea corecta. Daca specificati o valoare care este prea mare, GIS-ul poate sari la un alt vertex, in special cand lucrati cu un numar mare de vertexi apropriati unul de altul. Daca specificati cautarea radiala prea mica aplicatia GIS nu va gasi nici o entitate sau vertex de mutat sau de editat.

Probleme comune / lucruri de care trebuie să fiți conștienți¶

În principal sunt concepute pentru simplitate și pentru randare rapidă, dar nu și pentru analiza datelor care necesită topologie (cum ar fi găsirea rutelor într-o rețea). Multe aplicații GIS sunt capabile să prezinte împreună datele entităților simple și a celor topologice, iar unele, oferă chiar posibilitatea de a le crea, edita și analiza pe ambele.

Ce am învățat?¶

Să recapitulăm subiectele abordate în acest capitol:

• Topologia ne arată relaţia spaţială dintre entităţile vector vecine.

• Topologia în GIS poate fi accesată de către instrumentele topologice.

• Topologia poate fi utilizată pentru a detecta şi corecta erorile de digitizare

• Pentru anumite instrumente, precum analiza reţelei, datele topologice sunt estenţiale.

• Distanţa de snap şi raza de căutare ne ajută să digitizăm corect topologic datele vector.

• O entitate simplă nu reprezintă un adevărat format de date topologic, dar este frecvent utilizat de aplicațiile GIS.

Încercați acum!¶

Aici sunt câteva idei care pot fi testate împreună cu elevii dumneavoastră:

• Marcati opririle autobuzului local pe o harta topografica si apoi dati ca sarcina elevilor dumneavoastra sa gaseasca cea mai scurta cale dintre cele doua opriri.

• Gândiți-vă la modul în care ați crea entitățile vectoriale într-un GIS, pentru a reprezenta o rețea de drumuri topologice din orașul dvs. Ce reguli topologice sunt importante, și ce instrumente pot utiliza studenții dvs. în QGIS, pentru a vă asigura că noul strat cu drumuri este corect din punct de vedere topologic?

De reținut¶

Dacă nu aveți un calculator disponibil, puteți utiliza o hartă a rețelei de transport feroviar sau auto, apoi să discutați despre relațiile spațiale și despre topologie cu studenții.

Lecturi suplimentare¶

Cărți:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195

Site-uri web:

• http://www.innovativegis.com/basis/primer/concepts.html
• http://en.wikipedia.org/wiki/Geospatial_topology

Ghidul de utilizare QGIS conţine mai multe informaţii detaliate despre istrumentele de editare topologică.

Ce urmează?¶

In sectiunea care urmeaza vom arunca o privire de aproape asupra “Sistemelor de coordonate” pentru a intelege cum relationam datele despre pamantul sferic sferic si hartile plate.