Sistema di riferimento¶
 |
Obiettivi: |
Introduzione sui sistemi di riferimento. |
Parole chiave: |
Sistema di riferimento (SR), Proiezione cartografica, Proiezione al volo, Latitudine, Longitudine, Nord, Est |
Panoramica¶
Map projections try to portray the surface of the earth or a portion of the earth on a flat piece of paper or computer screen. A coordinate reference system (CRS) then defines, with the help of coordinates, how the two-dimensional, projected map in your GIS is related to real places on the earth. The decision as to which map projection and coordinate reference system to use, depends on the regional extent of the area you want to work in, on the analysis you want to do and often on the availability of data.
Dettagli sulle proiezioni cartografiche¶
Un metodo tradizionale per rappresentare la forma della Terra è l’uso dei globi. C’è, in ogni caso, un problema con questo approccio. Sebbene i globi conservino la maggior parte della forma della Terra e illustri la configurazione spaziale della geometria dei continenti, ci sono molte difficoltà nel portarli nella tasca di qualcuno. Inoltre, il loro uso è conveniente solo a scale estremamente piccole (per esempio 1:100 milioni)
La maggior parte dei dati per mappe tematiche comunemente utilizzate in applicazioni GIS sono di scala considerevolmente maggiore. Una tipica base dati GIS può avere scale da 1:250000 in su, a seconda del livello di dettaglio. Un globo di questa scala sarebbe costoso da produrre e ancor più da trasportare. Come risultato, i cartografi hanno sviluppato varie tecniche di proiezione cartografica per rappresentare, con ragionevole accuratezza, la superficie sferica della terra in due dimensioni.
Se vista da vicino la terra sembra essere relativamente piatta. Tuttavia, vista dallo spazio, si può notare come la terra sia relativamente sferica. Le mappe, come vedremo nel prossimo argomento sulla produzione cartografica, sono rappresentazioni della realtà. Esse sono progettate per rappresentare non solo degli oggetti territoriali, ma anche la relativa forma e disposizione spaziale. Ogni proiezione cartografica ha i suoi vantaggi e svantaggi. La miglior proiezione per una certa mappa dipende dalla sua scala e dai fini per cui essa sarà utilizzata. Una proiezione può ad esempio avere distorsioni inaccettabili se utilizzata per mappare l’intero continente africano, ma può essere una scelta eccellente per una mappa a grande scala (dettagliata) del vostro paese. Le proprietà di una proiezione cartografica possono influenzare alcune delle caratteristiche di design della mappa. Certe proiezioni sono valide per piccole aree, certe lo sono per descrivere zone con una grande estensione Est-Ovest, e certe altre sono le migliori per la descrizione di aree con una notevole estensione nord-sud.
Le tre famiglie di proiezioni cartografiche¶
The process of creating map projections can be visualised by positioning a light source inside a transparent globe on which opaque earth features are placed. Then project the feature outlines onto a two-dimensional flat piece of paper. Different ways of projecting can be produced by surrounding the globe in a cylindrical fashion, as a cone, or even as a flat surface. Each of these methods produces what is called a map projection family. Therefore, there is a family of planar projections, a family of cylindrical projections, and another called conical projections (see figure_projection_families)
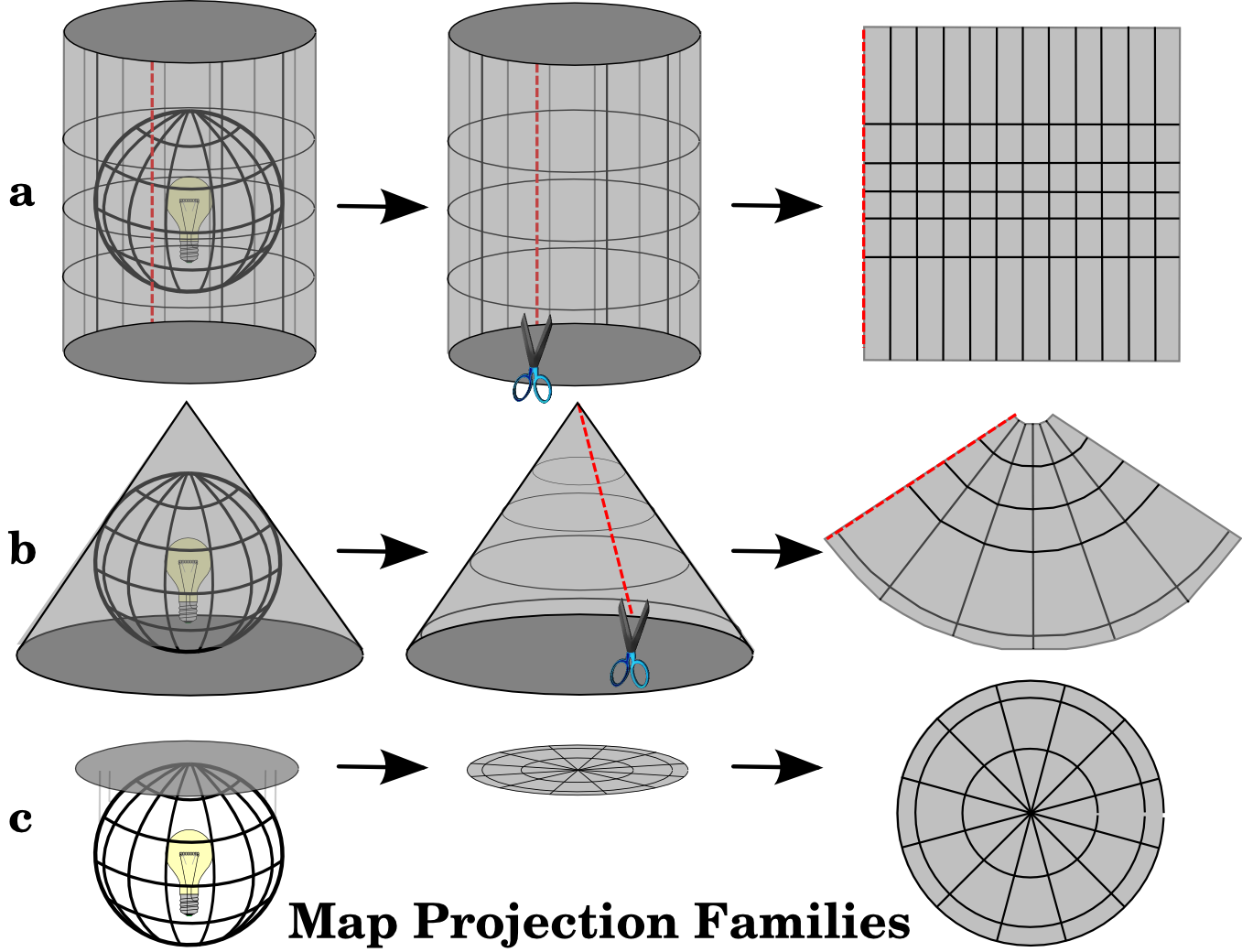
Le tre famiglie di proiezioni cartografiche. Possono essere rappresentate da a) proiezioni cilindriche, b) proiezioni coniche o c) proiezioni piane.
Naturalmente oggi il processo di proiezione della terra su un pezzo di carta è eseguito seguendo i principi matematici della geometria e della trigonometria. Questi processi ricreano la proiezione fisica della luce attraverso il globo trasparente.
Precisione delle proiezioni cartografiche¶
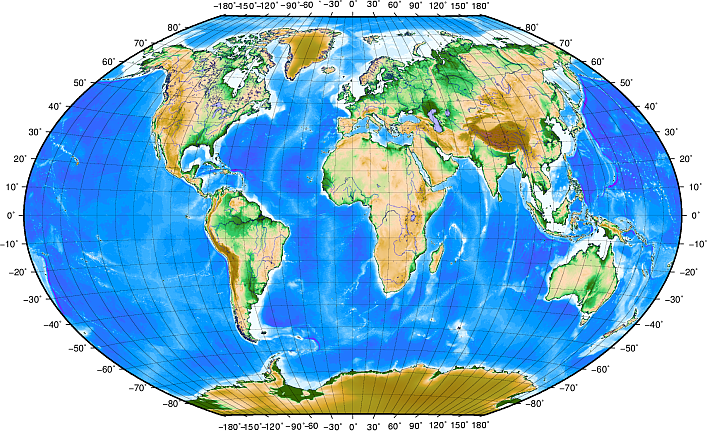
Map projections are never absolutely accurate representations of the spherical earth. As a result of the map projection process, every map shows distortions of angular conformity, distance and area. A map projection may combine several of these characteristics, or may be a compromise that distorts all the properties of area, distance and angular conformity, within some acceptable limit. Examples of compromise projections are the Winkel Tripel projection and the Robinson projection (see figure_robinson_projection), which are often used for world maps.

La proiezione di Robinson è un compromesso accettabile per le distorsioni di superficie, conformità angolare e di distanza.
Di solito è impossibile mantenere tutte le caratteristiche allo stesso tempo in una proiezione. Ciò significa che qualora si desideri effettuare operazioni analitiche accurate, sarà necessario utilizzare una proiezione cartografica che fornisca le migliori caratteristiche utili ai processi di analisi. Ad esempio, se vi è la necessità di misurare con precisione le distanze tra oggetti sulla mappa, bisognerà cercar di utilizzare una proiezione cartografica che fornisca un’elevata precisione sulle distanze.
Proiezioni cartografiche isogone o conformi¶
Quando si lavora con un globo, le direzioni principali sulla rosa dei venti (Nord, Est, Sud e Ovest) avranno tra di loro una distanza angolare sempre pari a 90 gradi. In altre parole, l’Est sarà sempre ad un angolo di 90 gradi rispetto al nord. Si possono mantenere delle proprietà angolari corrette anche in una proiezione cartografica. Una proiezione cartografica che mantiene le proprietà di conformità angolare è definita conforme o proiezione ortomorfica.
Questo tipo di proiezioni è usato quando è importante la conservazione delle relazioni angolari. Tali proiezioni sono comunemente utilizzate per le attività di navigazione o meteorologiche. È importante ricordare che per grandi aree è difficile il mantenimento di angoli veri su una mappa e che tale sistema di proiezione dovrebbe essere eseguito solo per piccole porzioni della terra. La proiezione conforme provoca la distorsione delle aree, il che significa che se le misure delle superfici sono fatte su una mappa, esse non saranno corrette. Più grande è l’area, meno accurate saranno le misure della sua superficie. La proiezione di Mercatore (come mostrato nella figure_mercator_projection) e la Proiezione conica conforme di Lambert sono degli esempi. Il servizio geologico USA utilizza una proiezione conforme per molte delle sue mappe topografiche.
Proiezioni cartografiche equidistanti¶
Se il vostro obiettivo nel proiettare una mappa è quello di misurare con precisione le distanze, sarà necessario selezionare una proiezione che sia stata progettata per preservare le distanze. Tali proiezioni, chiamate proiezioni equidistanti, richiedono che la scala della mappa sia mantenuta costante. Una mappa è equidistante qualora rappresenti correttamente le distanze dal centro della proiezione a qualsiasi altro punto sulla mappa. Le proiezioni equidistanti mantengono distanze corrette dal centro della proiezione o lungo determinate direzioni. Queste proiezioni sono utilizzate per mappature radio, per quelle sismiche e per la navigazione. La proiezione Plate Carrée cilindrica equidistante (vedi figure_plate_caree_projection) e la proiezione equirettangolare sono due buoni esempi di proiezioni equidistanti. La proiezione azimutale equidistante è la proiezione utilizzata per l’emblema delle Nazioni Unite (vedi figure_azimuthal_equidistant_projection).
Proiezioni equivalenti - mantenimento delle aree¶
When a map portrays areas over the entire map, so that all mapped areas have the same proportional relationship to the areas on the Earth that they represent, the map is an equal area map. In practice, general reference and educational maps most often require the use of equal area projections. As the name implies, these maps are best used when calculations of area are the dominant calculations you will perform. If, for example, you are trying to analyse a particular area in your town to find out whether it is large enough for a new shopping mall, equal area projections are the best choice. On the one hand, the larger the area you are analysing, the more precise your area measures will be, if you use an equal area projection rather than another type. On the other hand, an equal area projection results in** distortions of angular conformity** when dealing with large areas. Small areas will be far less prone to having their angles distorted when you use an equal area projection. Alber’s equal area, Lambert’s equal area and Mollweide Equal Area Cylindrical projections (shown in figure_mollweide_equal_area_projection) are types of equal area projections that are often encountered in GIS work.
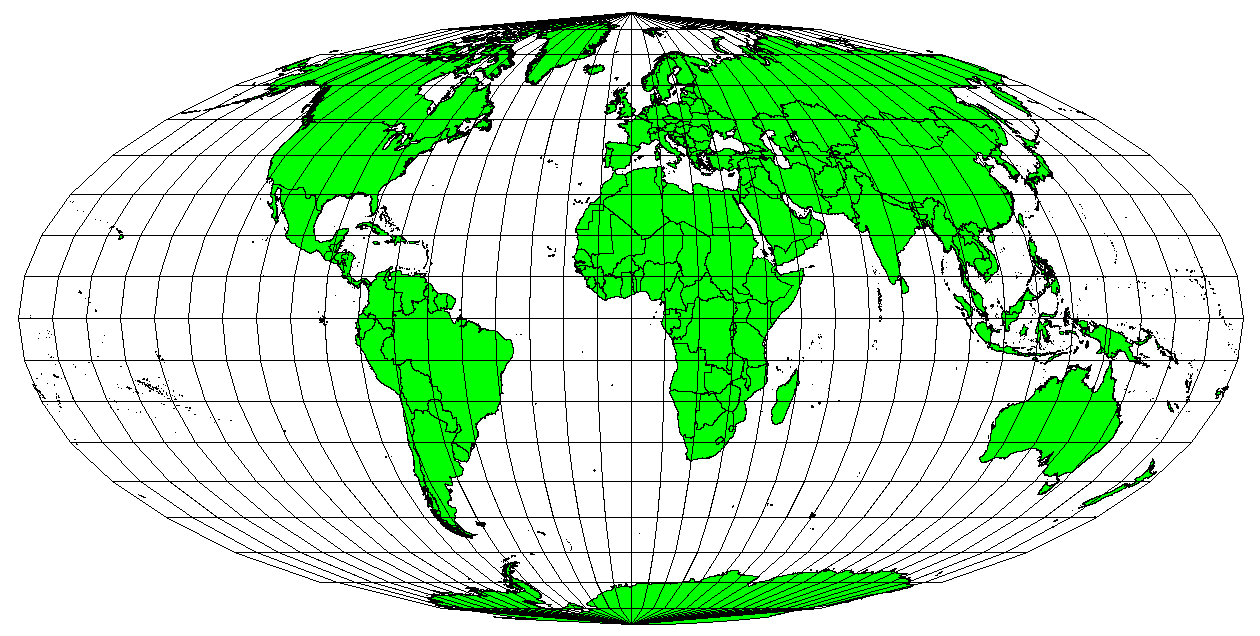
La Proiezione Cilindrica Equiareale Mollweide, ad esempio, assicura che tutte le aree cartografate abbiano la stessa relazione proporzionale con le relative aree sulla superficie terrestre.
Ricorda che le proiezioni sono un argomento molto complesso. Esistono centinaia di proiezioni diverse al mondo ed ognuna cerca di rappresentare una certa porzione di superficie terrestre, quanto più fedelmente possibile su una superficie piatta. In realtà la scelta della proiezione da usare dipende da te. Molte nazioni hanno proprie proiezione di uso comune e quando vengono scambiati dei dati le persone seguiranno il procedimento nazionale.
Sistema di riferimento (SR) nel dettaglio¶
Con l’aiuto dei sistemi di riferimento di coordinate (SR) ogni luogo sulla Terra può essere identificato da un insieme di tre numeri, definite coordinate. In generale, i SR possono essere suddivisi in sistemi di riferimento di coordinate proiettate (chiamati anche sistemi di riferimento di coordinate cartesiane o rettangolari) e sistemi di riferimento di coordinate geografiche.
Sistemi Coordinate Geografiche¶
L’utilizzo dei Sistemi di Riferimento è molto comune. Essi usano i gradi di latitudine e longitudine per descrivere una posizione sulla superficie terrestre. Il più noto è quello chiamato WGS 84.
Le linee di latitudine corrono parallele all’equatore e dividono la Terra in 180 sezioni da Nord a Sud (o da Sud a Nord). La linea di riferimento per la latitudine è l’equatore e ogni emisfero è diviso in novanta sezioni, ciascuna di un grado di latitudine. Nell’emisfero nord, i gradi di latitudine sono misurati da zero all’equatore a novanta al polo nord. Nell’emisfero sud, i gradi di latitudine sono misurati da zero all’equatore a novanta gradi al polo sud. Per semplificare la digitalizzazione delle mappe, ai gradi di latitudine nell’emisfero sud sono spesso assegnati valori negativi (da 0 a -90 °). Ovunque sulla superficie terrestre, la distanza tra le linee di latitudine è la stessa (60 miglia nautiche). Si veda la figura figure_geographic_crs.
Sistema di coordinate geografiche con linee di latitudine parallele all’equatore e linee di longitudine con il meridiano principale attraverso Greenwich.
Le linee di longitudine, d’altra parte, non reggono bene allo standard di uniformità. Le linee di longitudine corrono perpendicolarmente all’equatore e convergono ai poli. La linea di riferimento per la longitudine (il primo meridiano) va dal polo nord al polo sud attraverso Greenwich, in Inghilterra. Le successive linee di longitudine sono misurate da zero a 180 gradi est o ovest del primo meridiano. Si noti che ai valori ad ovest del primo meridiano da utilizzare nelle applicazioni di mappatura digitale sono assegnati valori negativi. Vedi figure_geographic_crs per una visualizzazione di insieme.
All’equatore, e solo all’equatore, la distanza rappresentata da una linea di longitudine è uguale alla distanza rappresentata da un grado di latitudine. Mentre ci si sposta verso i poli, la distanza tra le linee di longitudine diventa progressivamente minore, finché, nella posizione esatta del polo, tutti i 360 ° di longitudine sono rappresentati da un singolo punto su cui si potresti puntare il dito (probabilmente si dovresti però usare i guanti...). Usando il sistema di coordinate geografiche a livello di 1 grado, abbiamo una grigliato di linee che all’equatore divide la terra in quadrati che coprono circa 12363.365 chilometri quadri - un buon inizio, ma non molto utile per determinare la posizione di qualsiasi cosa all’interno di quel quadrato.
Per essere veramente utile, un grigliato della mappa deve essere divisa in sezioni abbastanza piccole in modo che possano essere utilizzate per descrivere (con un livello accettabile di accuratezza) la posizione di un punto sulla mappa. Per fare ciò, i gradi sono divisi in minuti (') e secondi ("). Ci sono sessanta minuti in un grado e sessanta secondi in un minuto (3600 secondi in un grado). Quindi, all’equatore, un secondo di latitudine o longitudine = 30,87624 metri.
Sistema di Riferimento proiettato¶
Un sistema di riferimento di coordinate bidimensionale è comunemente definito da due assi. Ad angolo retto tra loro, formano un cosiddetto piano XY (vedi figure_projected_crs sul lato sinistro). L’asse orizzontale è normalmente etichettato X e l’asse verticale è normalmente etichettato Y. In un sistema di riferimento di coordinate tridimensionale, viene aggiunto un altro asse, normalmente etichettato Z. È anch’esso ad angolo retto rispetto agli assi X e Y. L’asse Z fornisce la terza dimensione dello spazio (vedi figure_projected_crs sul lato destro). Ogni punto che è espresso in coordinate sferiche può essere espresso con una coordinata X Y Z.
Un sistema di riferimento di coordinate proiettate nell’emisfero sud (a sud dell’equatore) normalmente ha origine sull’equatore di una specifica Longitudine. Ciò significa che i valori Y aumentano verso sud e i valori X aumentano verso ovest. Nell’emisfero settentrionale (a nord dell’equatore) l’origine è anche l’equatore di una specifica Longitudine. Tuttavia, ora i valori Y aumentano verso nord e i valori X aumentano verso est. Nella sezione seguente, descriviamo un sistema di riferimento di coordinate proiettate chiamato Universal Transverse Mercator (UTM), spesso usato per il Sudafrica.
SR Universal Transverse Mercator (UTM) nel dettaglio¶
Il sistema di riferimento di coordinate Universal Transverse Mercator (UTM) ha la sua origine sull’equatore a una Longitudine specifica. Ora i valori Y aumentano verso sud e i valori X aumentano verso ovest. L’SR UTM è una proiezione cartografica globale. Ciò significa che viene generalmente utilizzato in tutto il mondo. Ma come già descritto nella sezione ‘accuratezza delle proiezioni cartografiche’ sopra, maggiore è l’area (ad esempio il Sud Africa) più si verificano distorsioni di conformità angolare, distanza e area. Per evitare troppe distorsioni, il mondo è diviso in 60 zone uguali che sono tutte di 6 gradi di larghezza in longitudine da est a ovest. Le zone UTM sono numerate da 1 a 60, a partire dalla linea di data internazionale (zona 1 a 180 gradi di longitudine ovest) e avanzando verso est fino alla linea di data internazionale (zona 60 a 180 gradi di longitudine est) come mostrato in figure_utm_zones.
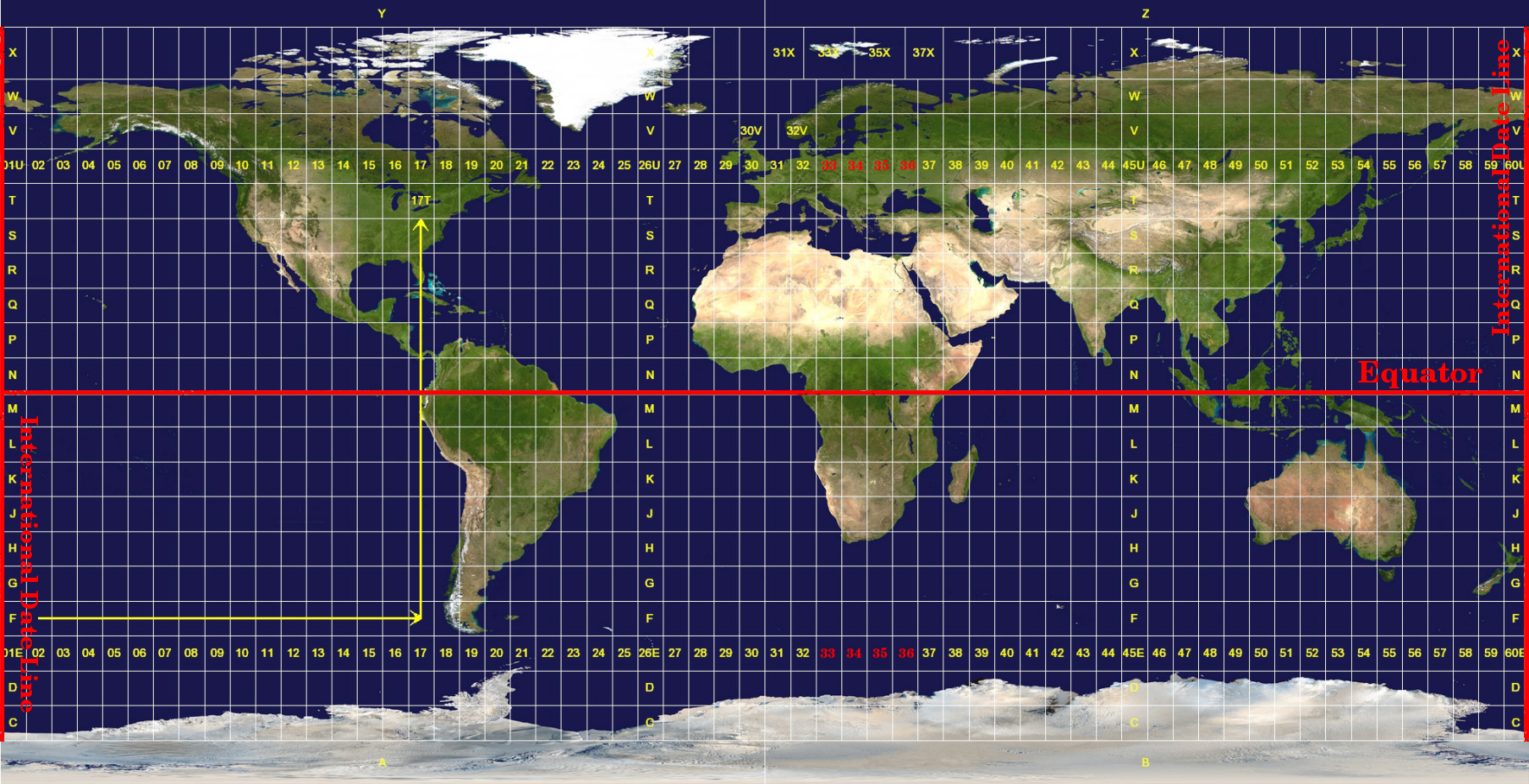
Le zone Universal Transverse Mercator. Per il Sudafrica vengono utilizzate le zone UTM 33S, 34S, 35S e 36S.
Come puoi vedere in figure_utm_zones e figure_utm_for_sa, il Sud Africa è coperto da quattro zone UTM per ridurre al minimo la distorsione. Le zone sono chiamate UTM 33S, UTM 34S, UTM 35S e UTM 36S. Il S dopo la zona indica che le zone UTM si trovano a sud dell’equatore.

Zone UTM 33S, 34S, 35S e 36S con le loro longitudini centrali (meridiani) utilizzate per proiettare il Sudafrica con elevata precisione. La X rossa mostra una Area of Interest (AOI).
Supponiamo, ad esempio, di voler definire una coordinata bidimensionale all’interno della Area di interesse (AOI) contrassegnata da una X rossa in figure_utm_for_sa. Puoi vedere che l’area si trova all’interno della zona UTM 35S. Ciò significa, per ridurre al minimo la distorsione e ottenere risultati di analisi accurati, dovremmo utilizzare UTM zone 35S come sistema di riferimento delle coordinate.
The position of a coordinate in UTM south of the equator must be indicated with the zone number (35) and with its northing (y) value and easting (x) value in meters. The northing value is the distance of the position from the equator in meters. The easting value is the distance from the central meridian (longitude) of the used UTM zone. For UTM zone 35S it is 27 degrees East as shown in figure_utm_for_sa. Furthermore, because we are south of the equator and negative values are not allowed in the UTM coordinate reference system, we have to add a so called false northing value of 10,000,000 m to the northing (y) value and a false easting value of 500,000 m to the easting (x) value. This sounds difficult, so, we will do an example that shows you how to find the correct UTM 35S coordinate for the Area of Interest.
The northing (y) value¶
The place we are looking for is 3,550,000 meters south of the equator, so the northing (y) value gets a negative sign and is -3,550,000 m. According to the UTM definitions we have to add a false northing value of 10,000,000 m. This means the northing (y) value of our coordinate is 6,450,000 m (-3,550,000 m + 10,000,000 m).
The easting (x) value¶
First we have to find the central meridian (longitude) for the UTM zone 35S. As we can see in figure_utm_for_sa it is 27 degrees East. The place we are looking for is 85,000 meters West from the central meridian. Just like the northing value, the easting (x) value gets a negative sign, giving a result of -85,000 m. According to the UTM definitions we have to add a false easting value of 500,000 m. This means the easting (x) value of our coordinate is 415,000 m (-85,000 m + 500,000 m). Finally, we have to add the zone number to the easting value to get the correct value.
Il risultato è che le coordinate per il nostro Punto di interesse proiettato nella zona UTM 35S dovrebbero essere scritte come: 35 415.000 m E / 6.450.000 m N. In alcuni GIS, quando viene definita la zona UTM corretta 35S e le unità sono impostate su metri all’interno del sistema, la coordinata potrebbe anche apparire semplicemente come 415.000 6.450.000.
Riproiezione al volo¶
Come puoi immaginare, potrebbe esserci una situazione in cui i dati che si desidera utilizzare in un GIS vengono proiettati in diversi sistemi di riferimento di coordinate. Ad esempio, potresti ottenere un layer vettoriale che mostra i confini del Sudafrica proiettati in UTM 35S e un altro layer vettoriale con informazioni puntuali sulle precipitazioni fornite nel sistema di coordinate geografiche WGS 84. In GIS questi due layer vettoriali sono posizionati in aree completamente diverse nella finestra della visualizzazione mappa, perché hanno proiezioni diverse.
Per risolvere questo problema molti GIS includono funzionalità chiamate riproiezione al volo. Questo significa che puoi definire una certa proiezione all’avvio del GIS e tutti i layer che caricherai verranno automaticamente visualizzati nella proiezione da te definita qualunque sia il loro sistema di riferimento delle coordinate. Questa funzionalità permette di sovrapporre layer nella finestra di mappa del tuo GIS, anche nel caso questi abbiano differenti Sistemi di Riferimento.
Problemi comuni / cose di cui essere consapevoli¶
L’argomento proiezione mappe è molto complesso e anche i professionisti che hanno studiato geografia, geodetica o qualsiasi altra scienza relativa al GIS, spesso hanno problemi con la corretta definizione di proiezioni cartografiche e sistemi di riferimento delle coordinate. Di solito quando lavori con GIS, hai già i dati proiettati per iniziare. Nella maggior parte dei casi, questi dati verranno proiettati in un determinato SR, quindi non è necessario creare un nuovo SR o persino proiettare i dati da un SR a un altro. Detto questo, è sempre utile avere un’idea di cosa significhi la proiezione cartografica e il SR.
Cosa abbiamo imparato?¶
Cerchiamo di riassumere gli argomenti che abbiamo affrontato in questo foglio di lavoro:
Le Proiezioni Mappa rappresentano la superficie della terra su una porzione piana bidimensionale di carta o sullo schermo del computer.
Esistono delle proiezioni di mappa globali, ma la maggior parte sono state create ed ottimizzate per piccole aree della superficie trerrestre.
Le Proiezioni di Mappa non sono mai rappresentazioni completamente accurate della terra sferica. Esse mostrano distorsioni di conformità angolare, di distanza e di area zona. È impossibile conservare tutte queste caratteristiche insieme in una proiezione.
Un Sistema di Riferimento (SR) definisce con il supporto delle coordinate come una mappa bidimensionale proiettata è in relazione con la localizzazione reale sulla superficie terrestre.
Esistono due diversi tipi di Sistemi di Riferimento: Sistemi di Riferimento Geografici e Sistemi di Riferimento Proiettati.
La proiezione al volo è una funzionalità GIS che permette di sovrapporre tra loro layer anche se proiettati in diversi Sistemi di Riferimento delle coordinate
Adesso prova tu!¶
Ecco alcune idee per provare con i vostri studenti:
Avvia QGIS e carica due layer della stessa area ma con proiezioni diverse e consenti ai tuoi alunni di trovare le coordinate di più posizioni sui due layer. Puoi mostrare loro che non è possibile sovrapporre i due layer. Quindi definire il sistema di riferimento delle coordinate come Geografico/WGS 84 all’interno della finestra di dialogo Proprietà progetto... e attivare la casella di controllo
 Effettua la trasformazione ‘al volo’ del SR (OTF). Carica di nuovo i due layer della stessa area e lascia che i tuoi studenti vedano come funziona la proiezione al volo.
Effettua la trasformazione ‘al volo’ del SR (OTF). Carica di nuovo i due layer della stessa area e lascia che i tuoi studenti vedano come funziona la proiezione al volo.Puoi aprire la finestra di dialogo Proprietà progetto... in QGIS e mostrare ai tuoi studenti i diversi sistemi di riferimento di coordinate in modo da dare loro un’idea della complessità di questo argomento. Con la trasformazione CRS ‘al volo’ attivata è possibile selezionare SR diversi per visualizzare lo stesso layer in diverse proiezioni.
Qualcosa su cui pensare¶
If you don’t have a computer available, you can show your pupils the principles of the three map projection families. Get a globe and paper and demonstrate how cylindrical, conical and planar projections work in general. With the help of a transparency sheet you can draw a two-dimensional coordinate reference system showing X axes and Y axes. Then, let your pupils define coordinates (x and y values) for different places.
Ulteriori link¶
Libri:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. Terza edizione. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. Terza edizione. Wiley. ISBN: 9814126195
- Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X
Siti web:
- http://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html
- http://geology.isu.edu/geostac/Field_Exercise/topomaps/index.htm
La Guida dell’utente di QGIS contiene informazioni maggiormente dettagliate per lavorare con le proiezioni di mappa in QGIS.
Cosa viene adesso?¶
Nella prossima sezione andremo a vedere in modo più approfondito alla Produzione di Mappe



