Datos Vectoriales¶

Vista general¶

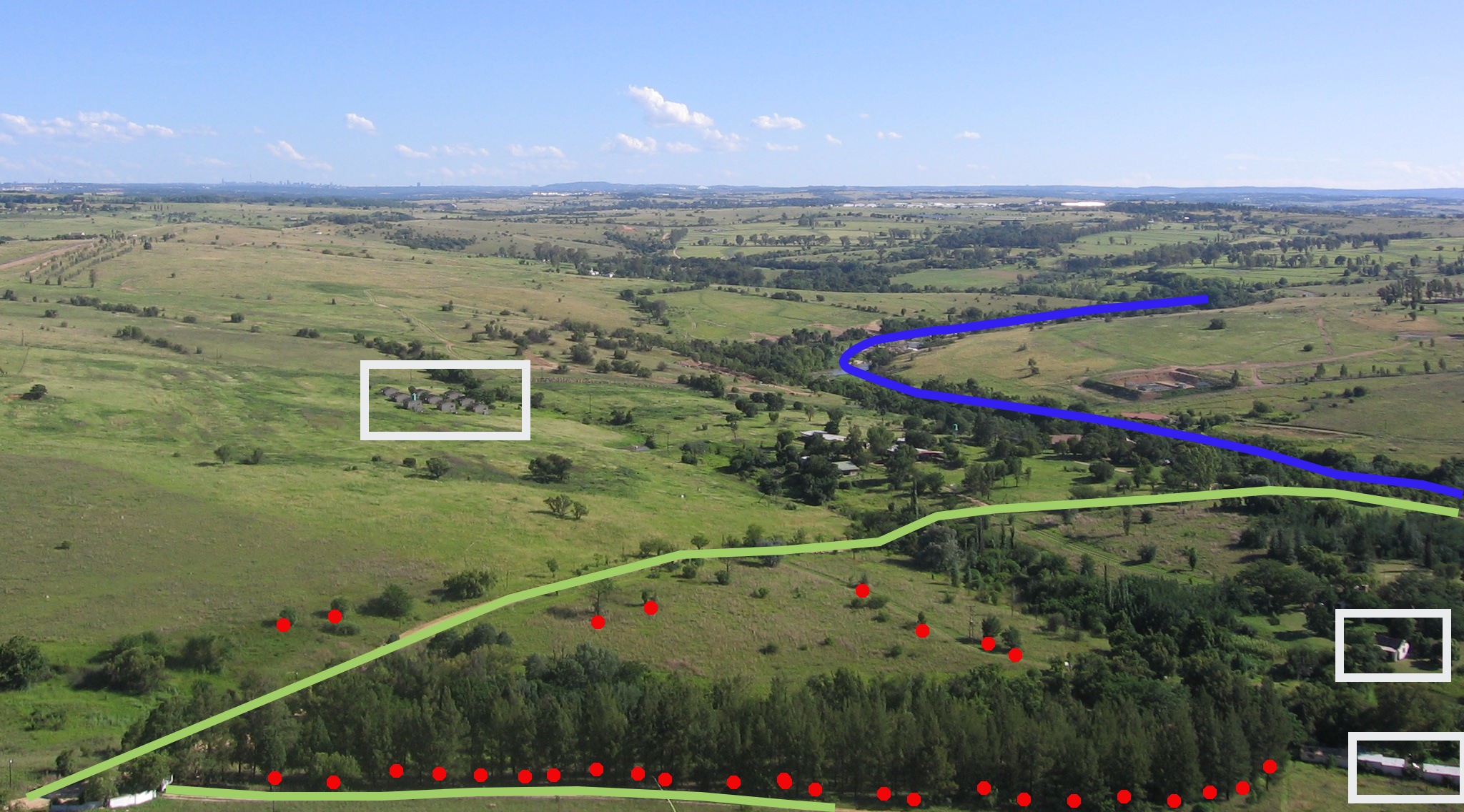
Vector data provide a way to represent real world features within the GIS environment. A feature is anything you can see on the landscape. Imagine you are standing on the top of a hill. Looking down you can see houses, roads, trees, rivers, and so on (see figure_vector_landscape). Each one of these things would be a feature when we represent them in a GIS Application. Vector features have attributes, which consist of text or numerical information that describe the features.

Observando un paisaje, se pueden apreciar objetos tales como carreteras, casas y árboles.

A vector feature has its shape represented using geometry. The geometry is made up of one or more interconnected vertices. A vertex describes a position in space using an X, Y and optionally z axis. Geometries which have vertices with a Z axis are often referred to as 2.5D since they describe height or depth at each vertex, but not both.

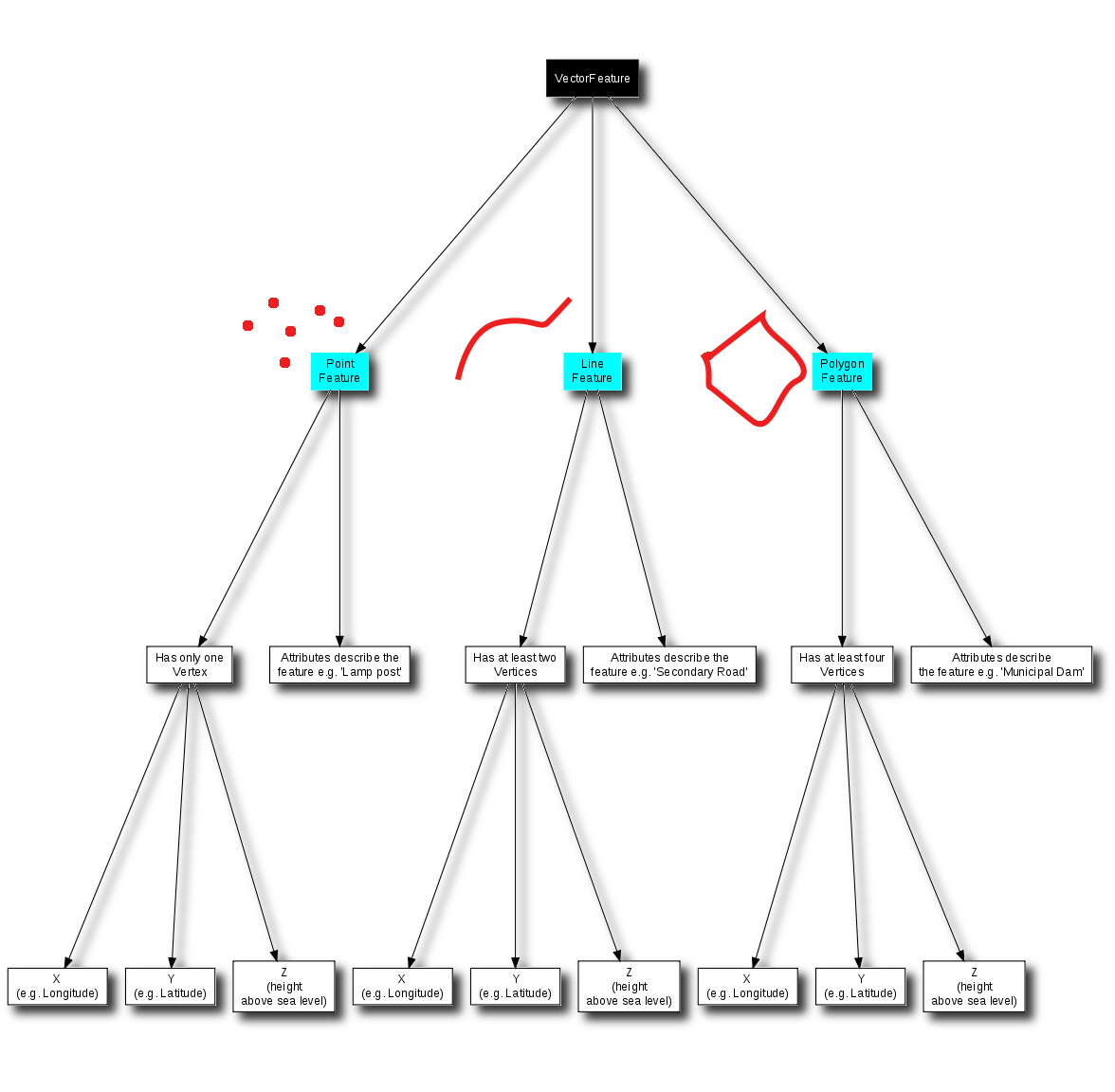
Cuando la geometría de una objeto espacial consiste en un solo vértice, se conoce como una elemento punto (véase la ilustración figure_geometry_point). Cuando la geometría consiste en dos o más vértices y el primer y último vértice no son iguales, un elemento polilínea se forma (ver ilustración figure_geometry_polyline). Cuando tres o más vértices están presentes, y el último vértice es igual a la primero, un elemento polígono se forma (vea la ilustración figure_geometry_polygon).

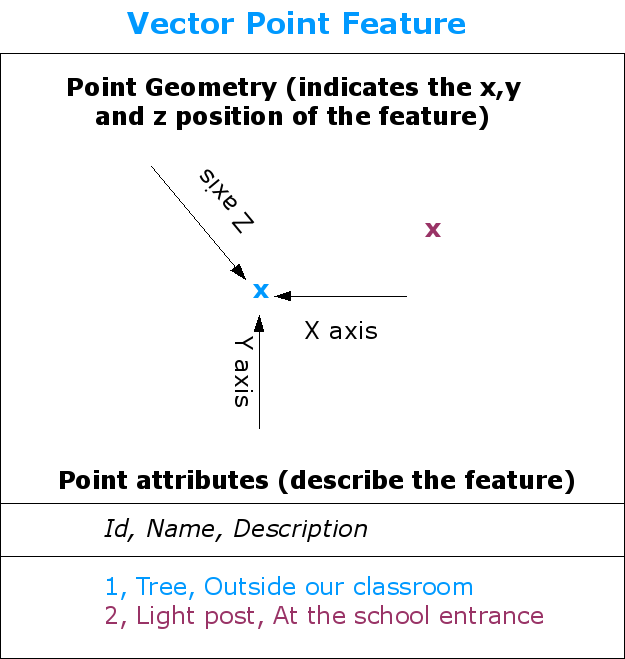
Un objeto de tipo punto se describe por sus coordenas X, Y y opcionalmente Z. El punto es descrito mediante atributos como por ejemplo si se trata de un árbol o una farola.

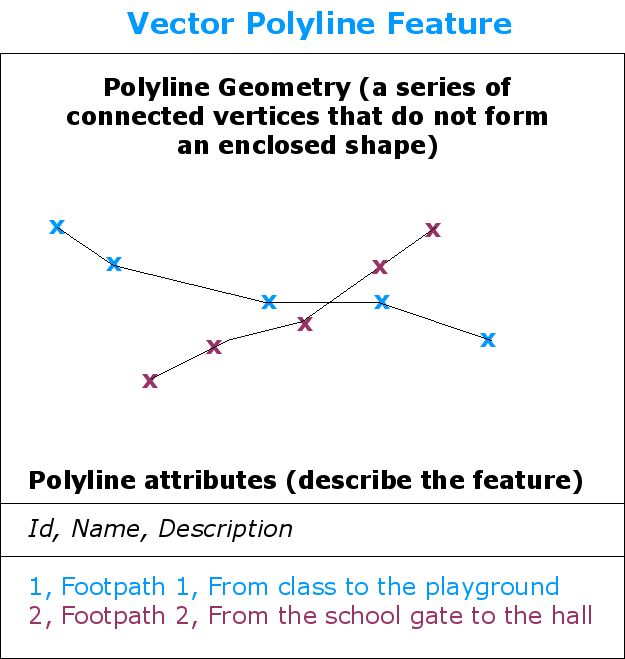
Una polilínea es una secuencia de vértices unidos. Cada vértice posee unas coordenadas X e Y (y opcionalmente Z). Los atributos describen la polilínea.

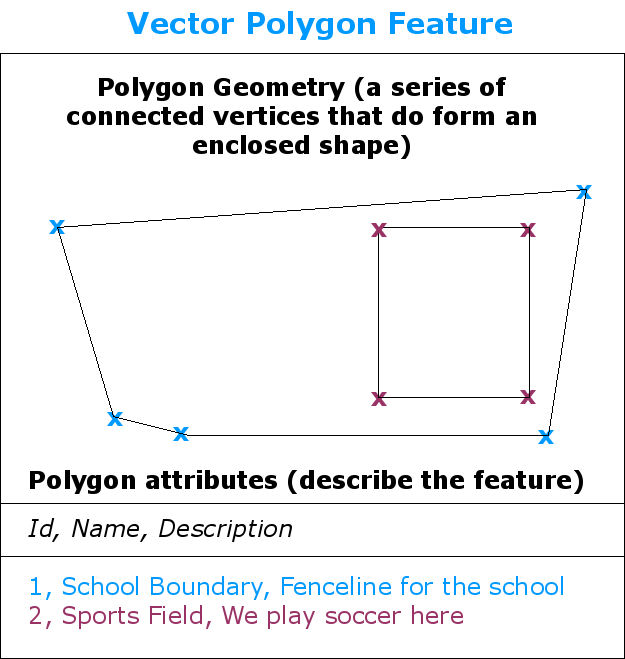
Un polígono, al igual que una polilínea, es una secuencia de vértices. Sin embargo, en un polígono el primer y último vértices se localizan siempre en la misma posición.

Mirando hacia atrás en la imagen de un paisaje que le mostramos más arriba, debería ser capaz de ver los diferentes tipos de objetos en la forma en que un SIG los representa ahora (ver ilustración figure_geometry_landscape).

Los objetos espaciales del paisaje como nos gustaría presentarlos en un SIG. Ríos (azul) y carreteras (verde) pueden ser representados como líneas, árboles como puntos (rojo) y casas como polígonos (blanco).

Los objetos de tipo punto en detalle¶

Lo primero que tenemos que darnos cuenta cuando cuando hablamos de objetos espaciales puntuales es que lo que describimos como un punto en el SIG es una cuestión de opinión, y a menudo depende de la escala. veamos a las ciudades, por ejemplo. Si usted tiene un mapa a escala pequeña (que cubre una área grande), puede tener sentido representar una ciudad utilizando un objeto puntual. Sin embargo, como el zum en el mapa, avanzar hacia una mayor escala, tiene más sentido mostrar los límites de la ciudad como un polígono.

Cuando elija utilizar los puntos para representar un objeto espacial es sobre todo una cuestión de escala (a qué distancia se encuentran del objeto), comodidad (se tarda menos tiempo y esfuerzo para crear entidades de puntos que las entidades poligonales), y el tipo de objeto espacial (algunas cosas como postes de teléfono simplemente no tienen sentido almacenarlas como polígonos).

Como mostramos en la ilustración figure_geometry_point, un punto tiene un valor X, Y y opcionalmente Z. Los valores X y Y dependerán del Sistema de Referencia de Coordenadas (SRC) que se utiliza. Vamos a entrar en más detalle acerca de los sistemas de referencia de coordenadas en un tutorial más adelante. Por ahora vamos simplemente a decir que un SRC es una manera de describir con precisión dónde está un lugar en particular sobre la superficie de la tierra. Uno de los sistemas de referencia más comunes es Longitud y Latitud. Líneas de Longitud van del Polo norte al Polo sur. Líneas de Latitud van de Este a Oeste. Se puede describir con precisión dónde se encuentra algún lugar de la tierra, dando su Longitud (X) y Latitud (Y). Si realiza una medición similar para un árbol o un poste de teléfono y lo marca en un mapa, habrá creado una entidad de punto.

Ya que sabemos que la tierra no es plana, a menudo es útil añadir un valor de Z a una entidad puntual. Esto describe qué tan alto sobre el nivel del mar se encuentra.

Los objetos polilínea en detalle¶

Cuando un elemento punto es un sólo vértice, una polilínea tiene dos o mas vértices. La polilínea es una ruta continua trazada a través de cada vértice, como muestra en figure_geometry_polyline. Cuando dos vértices están unidos, una línea es creada. Cuando mas de dos están unidos, forman una ‘línea de líneas’ o polilínea

Una polilínea se utiliza para mostrar la geometría de las entidades lineales como las carreteras, los ríos, las curvas de nivel, senderos, rutas de vuelo y así sucesivamente. A veces tenemos reglas especiales para polilíneas, además de su geometría básica. Por ejemplo las curvas de nivel pueden tocar (por ejemplo, en un acantilado), pero nunca deben cruzar entre sí. Del mismo modo, polilíneas utilizados para almacenar una red de carreteras deben conectarse en las intersecciones. En algunas aplicaciones SIG se pueden establecer estas reglas especiales para un tipo de entidad (por ejemplo, carreteras) y el SIG se asegurará de que estas polilíneas siempre cumplan con estas normas.

Si una polilínea curva tiene distancias muy grandes entre vértices, puede parecer angular o irregular, dependiendo de la escala a la que se vea (ver figure_polyline_jagged). Debido a esto, es importante que las polilíneas se digitalizen (capturado en la computadora) con distancias entre vértices que sean lo suficientemente pequeña para la escala en la que desea utilizar los datos.

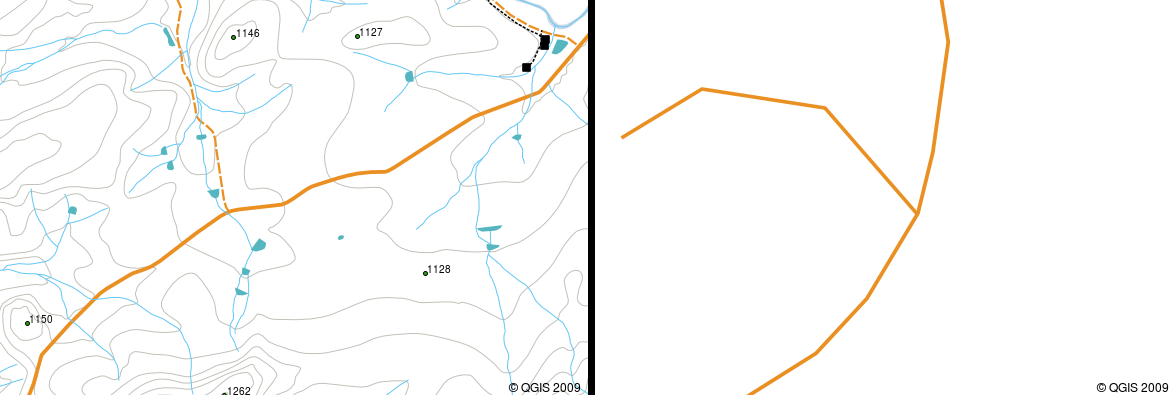
Polilíneas vistos a una escala menor (1:20 000 a la izquierda) pueden aparecer lisa y curvada. Cuando el zum a una mayor escala (1: 500 a la derecha) las polilíneas pueden parecer muy angular.

Los atributos de cada polilínea describe las propiedades o características. Por ejemplo una polilínea de carretera puede tener atributos que describan si es una superficie de grava o alquitrán, cuantos carriles tiene, si es un camino, calle, etc. El SIG puede utilizar estos atributos para simbolizar la entidad de polilínea con un color adecuado o estilo de línea

Objetos de tipo polígono en detalle¶

Las entidades poligonales son zonas cerradas como presas, islas, limites del país, etc. Como las entidades de polilínea, los polígonos se crean de una serie de vértices que se conectan con una línea continua. Sin embargo, debido a que un polígono siempre describe un área cerrada, ¡el primer y último vértice deberán siempre estar en el mismo lugar! Los polígonos regularmente tienen geometría compartida —- limites que tienen en común con un polígono vecino. Muchas aplicaciones SIG tienen la capacidad para asegurar que los limites de los polígonos vecinos coinciden exactamente. Nosotros examinaremos el tema Topología más adelante en este tutoríal

Como con los puntos y las polilíneas, los polígonos poseen attributes. Los atributos describen cada polígono. Por ejemplo, una presa podría tener atributos de profundidad y calidad del agua.

Datos vectoriales en capas¶

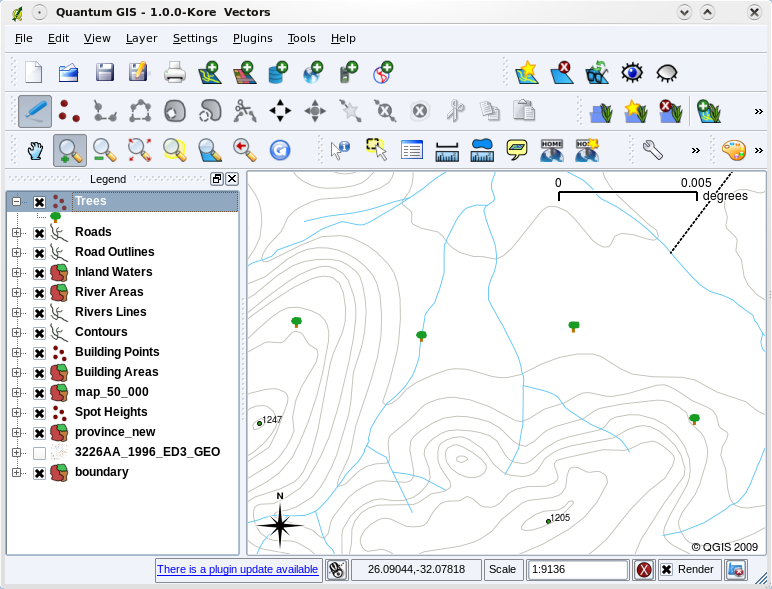
Now that we have described what vector data is, let’s look at how vector data is managed and used in a GIS environment. Most GIS applications group vector features into layers. Features in a layer have the the same geometry type (e.g. they will all be points) and the same kinds of attributes (e.g. information about what species a tree is for a trees layer). For example if you have recorded the positions of all the footpaths in your school, they will usually be stored together on the computer hard disk and shown in the GIS as a single layer. This is convenient because it allows you to hide or show all of the features for that layer in your GIS application with a single mouse click.

Edición de datos vectoriales¶

La aplicación SIG le permitirá crear y modificar los datos de la geometría en una capa — un proceso llamado digitalización — que vamos a ver más de cerca en un tutorial más tarde. Si una capa contiene polígonos (por ejemplo, presas agrícolas), la aplicación SIG sólo le permitirá crear nuevos polígonos en esa capa. Del mismo modo, si usted desea cambiar la forma de un objeto espacial, la aplicación sólo le permitirá hacerlo si la forma cambiada es correcta. Por ejemplo, no le permitirá editar una línea de tal manera que sólo tenga un vértice — recuerde en nuestra discusión de las líneas anteriores que todas las líneas deben tener al menos dos vértices.

Creación y edición de datos vectoriales es una función importante de un SIG, ya que es una de las principales formas en que se pueden crear datos de carácter personal por las cosas que le interesan. Digamos por ejemplo que está supervisando la contaminación en un río. Se podría utilizar el SIG para digitalizar todos los emisarios de desagüe de aguas pluviales (como una entidad de puntos). También puede digitalizar el río en sí (como una entidad de polilínea). Por último se puede tomar lecturas de los niveles de pH a lo largo del curso del río y digitalizar los lugares en que haya realizado estas lecturas (como una capa de puntos).

Así como la creación de sus propios datos, hay una gran cantidad de datos vectoriales gratis que se puede obtener y utilizar. Por ejemplo, se pueden obtener datos vectoriales que aparece en las hojas 1:50 000 de mapas de la Dirección Principal: Topografía y Cartografía.

Escala y datos vectoriales¶

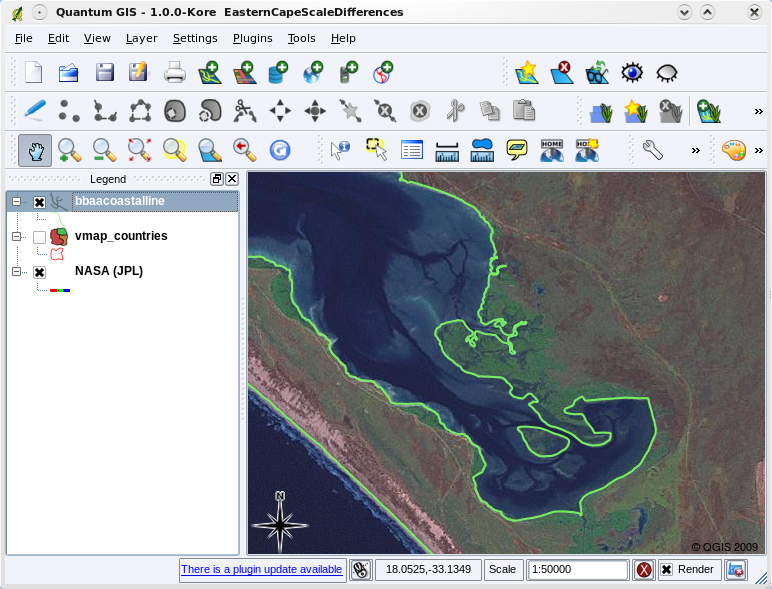
escala de mapa es un importante punto a considerar cuando se trabaja con datos vectoriales en un SIG. Cuando se capturan datos, por lo general digitalización de mapas existentes, o tomando información de los registros topográficos y dispositivos de sistemas de posicionamiento global. Los mapas tienen diferentes escalas, así que si importa datos vectoriales de un mapa a un entorno SIG (por ejemplo al digitalizar mapas en papel), los datos vectoriales digitales tendrán los mismos problemas de escala que el original. Este efecto se puede ver en las ilustraciones figure_vector_small_scale y figure_vector_large_scale. Muchos problemas pueden surgir de hacer una mala elección de la escala de mapa. Por ejemplo el uso de los datos vectoriales en la ilustración figure_vector_small_scale para planificar un área de conservación de humedales podría resultar ¡que partes importantes del humedal quedan fuera de la reserva! Por otro lado si esta tratando de crear un mapa regional, utilizar datos capturados a escala 1:1000 000 podría estar bien esto va a ahorrar mucho tiempo y esfuerzo de captura de datos.

Datos vectoriales (lineas rojas) que fueron difitalizadas desde una escala pequeña de mapa(1:1000 000).

Datos vectoriales (lineas verdes) que fueron digitalizadas de una escala grande de mapa (1:50 000).

Simbología¶

Al añadir las capas vectoriales a la vista del mapa en una aplicación SIG, estas se dibujaran con colores al azar y símbolos básicos. Una de las grandes ventajas de utilizar un SIG es que puede crear mapas personalizados muy fácilmente. El programa SIG le permitirá elegir los colores del tipo de entidad (por ejemplo,)

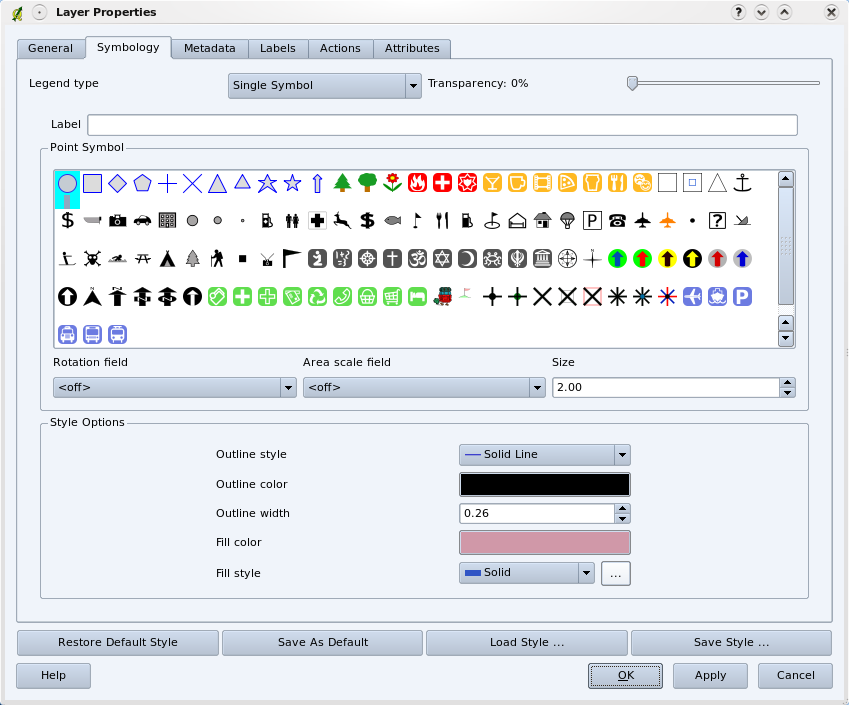
En el GIS, se puede utilizar un panel (como la de arriba) para determinar como deben dibujarse los objetos espaciales en su capa.

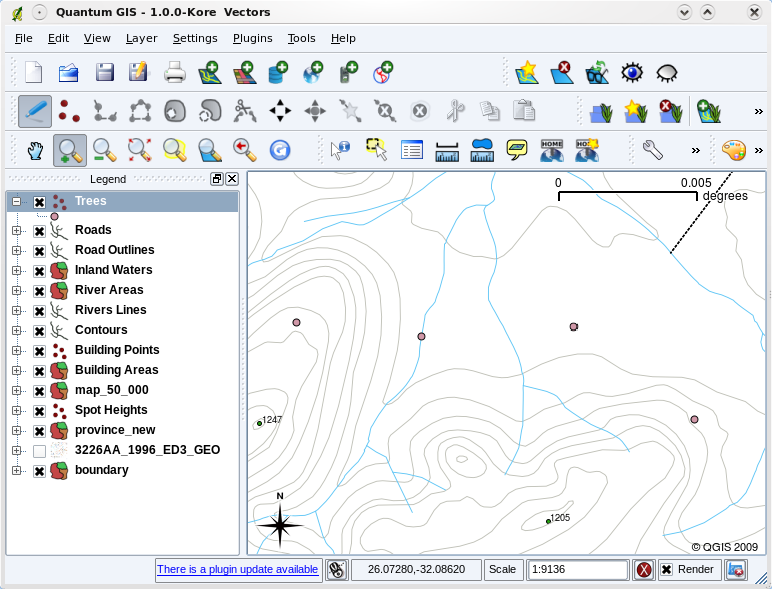
Cuando una capa (por ejemplo la capa de arboles anterior) se cargo primero, una aplicación SIG le dará un símbolo generico.

Después de hacer los ajustes es mucho más fácil ver que los puntos representan árboles.

La simbología es una característica de gran alcance, haciendo mapas más reales y los datos de su GIS más fácil de entender. En el tema que sigue (Datos de atributo de vector) vamos a examinar más profundamente cómo la simbología puede ayudar al usuario a entender los datos vectoriales.

¿Qué se puede lograr con los datos vectoriales en SIG?¶

Al nivel más simple podemos utilizar datos vectoriales en una aplicación SIG de la misma manera que utilizaría un mapa topográfico normal. El verdadero poder de los SIG comienza a manifestarse cuando se empieza a hacer preguntas como ‘¿qué casas están dentro del nivel de inundación de 100 años de un río?’; ‘¿dónde está el mejor lugar para poner un hospital para que sea fácilmente accesible a la mayor cantidad de gente posible?’; ‘¿qué alumnos viven en un suburbio particular?’. Un SIG es una gran herramienta para responder a este tipo de preguntas con la ayuda de los datos vectoriales. Generalmente nos referimos al proceso de responder a este tipo de preguntas como análisis espacial. En temas posteriores de este tutorial vamos a ver el análisis espacial con más detalle.

Problemas usuales con datos vectoriales¶

Trabajar con datos vectoriales tiene algunos problemas. Ya hemos mencionado los problemas que pueden surgir con los vectores capturados en diferentes escalas. Los datos vectoriales también necesita mucho trabajo y de mantenimiento para asegurar que sea exacta y fiable. Los datos vectoriales incorrectos pueden tener lugar cuando los instrumentos utilizados para capturar los datos no están debidamente establecidos, cuando las personas que capturan los datos no están siendo cuidadosos, cuando el tiempo o el dinero no permiten suficiente detalle en el proceso de recolección, etc.

Si se tienen datos vectoriales de mala calidad, a menudo se puede detectar este al ver los datos en un SIG. Por ejemplo slivers pueden ocurrir cuando los bordes de dos áreas de polígonos no se unen correctamente (ver figure_vector_slivers).

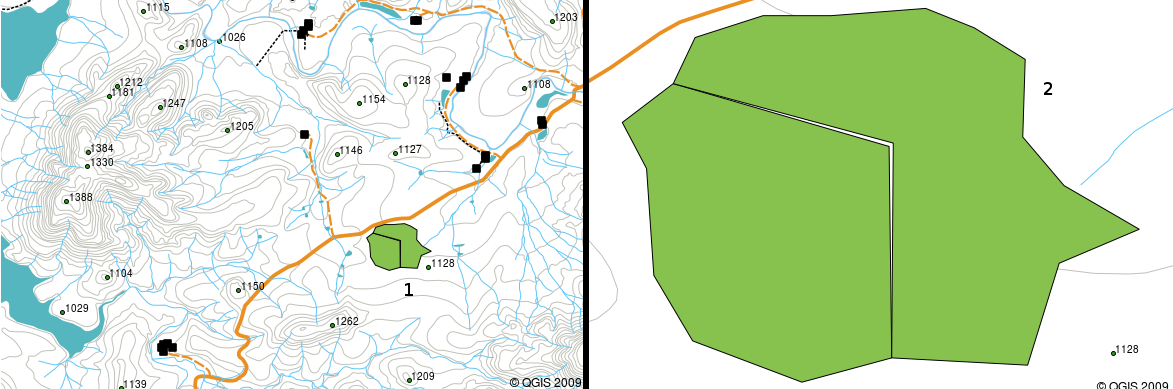
Los slivers ocurren cuando los vértices de dos polígonos no coinciden en sus fronteras. A una pequeña escala (por ejemplo 1 a la izquierda) es posible que no sea capaz de ver estos errores. A una gran escala, son visibles como tiras finas entre dos polígonos (2 a la derecha).

Overshoots can occur when a line feature such as a road does not meet another road exactly at an intersection. Undershoots can occur when a line feature (e.g. a river) does not exactly meet another feature to which it should be connected. Figure figure_vector_shoots demonstrates what undershoots and overshoots look like.

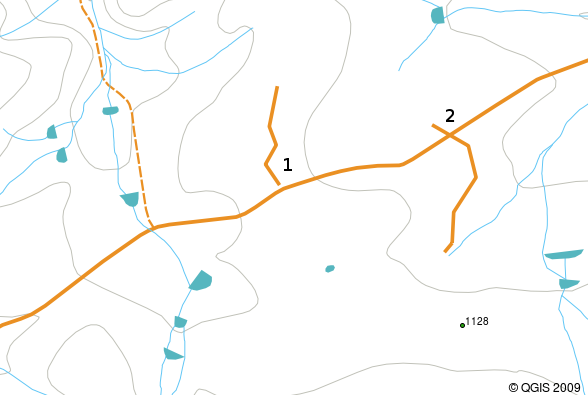
Undershoots (1) ocurre cuando las líneas vectoriales digitalizadas que deben conectarse con otras no hacen contacto del todo. Overshoots (2) ocurren si una línea termina más allá de la línea a la que debe conectarse.

Debido a este tipo de errores, es muy importante digitalizar los datos cuidadosamente y con precisión. En el próximo tema topología vamos a revisar algunos de estos tipos de errores en mayor detalle.

¿Qué hemos aprendido?¶

Vamos a concluir lo que hemos cubierto en esta hoja de trabajo:

• Datos vectoriales se utilizan para representar el mundo real objetos espaciales en un GIS.

• Un objeto espacial vectorial puede tener un tipo geometría de punto, línea o un polígono.

• Cada objeto espacial vectorial tienen datos de atributos que lo describen.

• La geometría del objeto espacial esta descrito en términos de vértices.

• Las geometrías puntuales se componen de un único vértice (X,Y y Z opcional)

• Las geometrías de polilineas se componen de dos o más vértices formando una línea conectada.

• Las geometrías de polígonos se componen de al menos cuatro vértices formando un área cerrada. El primer y último vértice están siempre en el mismo lugar.

• Elegir qué tipo de geometría a utilizar depende de la escala, la conveniencia y lo que quiere hacer con los datos en el SIG.

• La mayoría de las aplicaciones SIG no le permiten mezclar más de un tipo de geometría en una sola capa.

• Digitalizar es el proceso de creación de datos vectoriales digitales dibujándolo en una aplicación SIG.

• Los datos vectoriales pueden tener problemas de calidad tales como undershoots, overshoots y slivers que necesita tener en cuenta.

• Los datos vectoriales pueden ser utilizados para análisis espacial en una aplicación SIG, por ejemplo para encontrar el hospital más cercano a una escuela.

Hemos resumido el concepto de Dato Vectorial SIG en la figura figure_vector_summary.

Este diagrama muestra como las aplicaciones SIG trabajan con los datos vectoriales.

¡Pruebe usted ahora!¶

Aquí están algunas ideas para que intente con sus alumnos:

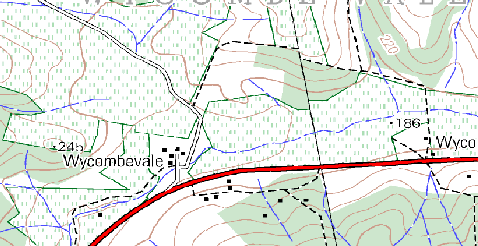
• Utiliza una copia de mapa topográfico para su área local (como se muestra uno en figure_sample_map), vea si sus estudiantes pueden identificar ejemplos de diferentes tipos de datos vectoriales al resaltarlos en el mapa.

• Piense cómo crearía elementos vectoriales en un SIG para representar los objetos espaciales del mundo real en sus terrenos escolares. Crear una tabla de diferentes elementos de los alrededores de su escuela y luego de la tarea a sus alumnos para decidir si estarían mejor representados en el SIG como un punto, línea o polígono. Vea un ejemplo table_vector_1.

¿Puede identificar dos objetos espaciales puntuales y un poligonal en este mapa?

Tabla vectorial 1: Crear una tabla como esta (dejar la columna de tipo de geometría vacío) y pedir a sus alumnos decidan el tipo de geometría adecuada.

Algo para pensar¶

Si no se tienen una computadora disponible, puede utilizar una carta topográfica y una hoja transparente para mostrar a sus alumnos acerca de los datos vectoriales.

Otras lecturas¶

La guía de usuario de QGIS también tiene información más detallada sobre como trabajar con datos vectoriales en QGIS.

¿Qué sigue?¶

En la sección siguiente, daremos una mirada más cercana a datos de atributos para ver cómo se puede utilizar para describir objetos espaciales vectoriales.