Sistema de coordenadas de referencia¶

Vista general¶

Map projections try to portray the surface of the earth or a portion of the earth on a flat piece of paper or computer screen. A coordinate reference system (CRS) then defines, with the help of coordinates, how the two-dimensional, projected map in your GIS is related to real places on the earth. The decision as to which map projection and coordinate reference system to use, depends on the regional extent of the area you want to work in, on the analysis you want to do and often on the availability of data.

Proyección cartográfica en detalle¶

Un método tradicional para representar la forma de la tierra es el uso del globo. Hay, sin embargo, un problema con este enfoque. Aunque los globos conservan la mayor parte de la forma de la tierra e ilustran la configuración espacial de objetos de tamaño continental, son muy difíciles de llevar en el bolsillo. También es conveniente solo utilizarlas en escalas pequeñas (por ejemplo, 1:100 millones).

La mayoría de los datos de los mapas temáticos de uso común en aplicaciones SIG son de escala considerablemente mayor. El típico conjunto de datos SIG utiliza escalas de 1:250 000 o mayor, dependiendo del nivel de detalle. Un globo de este tamaño sería difícil y caro de producir y aún más difícil de llevar. Como resultado, los cartógrafos han desarrollado un conjunto de técnicas llamadas proyecciones cartográficas diseñadas para mostrar, con una precisión razonable, la Tierra esférica en dos dimensiones.

Cuando se observa de cerca, la Tierra parece ser relativamente plana. Sin embargo, cuando se observa desde el espacio, podemos ver que es relativamente esférica. Los mapas, como veremos en el siguiente punto sobre elaboración de mapas, son representaciones de la realidad. Están diseñados no sólo para representar objetos, sino también su forma y distribución espacial. Cada mapa cartográfico presenta ventajas e inconvenientes. La mejor proyección para un mapa dependerá de la escala del mapa, y de los propósitos con los que se va a utilizar. Por ejemplo, un proyección podría presentar distorsiones inaceptables si se utiliza para mapear todo el continente Africano, pero podría ser una elección excelente para un mapa de alto detalle de un país. Las propiedades de un mapa cartográfico pueden también influenciar algunas de las características de diseño del mapa. Algunas proyecciones son buenas para pequeños espacos, otras son mejores para espacios con una gran componente Este-Oeste, y otras son mejores para espacios con una gran componente Norte-Sur.

Las tres familias de proyecciones cartográficas¶

The process of creating map projections can be visualised by positioning a light source inside a transparent globe on which opaque earth features are placed. Then project the feature outlines onto a two-dimensional flat piece of paper. Different ways of projecting can be produced by surrounding the globe in a cylindrical fashion, as a cone, or even as a flat surface. Each of these methods produces what is called a map projection family. Therefore, there is a family of planar projections, a family of cylindrical projections, and another called conical projections (see figure_projection_families)

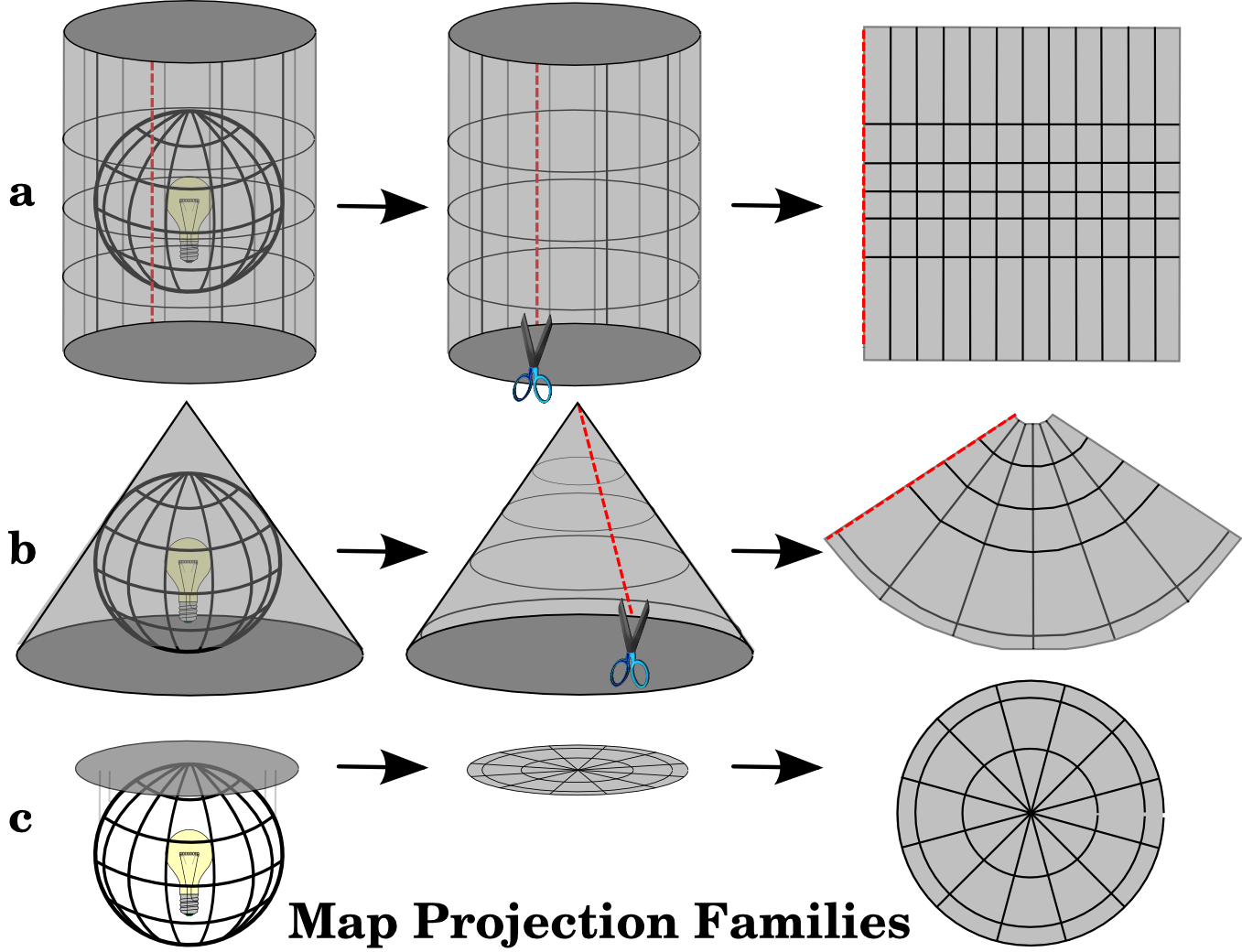
Las tres familias de proyecciones cartográficas. Pueden ser representadas por a) proyecciones cilíndricas, b) proyecciones cónicas o c) proyecciones planas.

Hoy en día, por supuesto, el proceso de proyectar la esfera terrestre sobre el papel se realiza utilizando los principios matemáticos de la geometría y la trigonometría. Este procedimeinto recrea la proyección de la luz a través del globo.

Precisión de los mapas cartográficos¶

Map projections are never absolutely accurate representations of the spherical earth. As a result of the map projection process, every map shows distortions of angular conformity, distance and area. A map projection may combine several of these characteristics, or may be a compromise that distorts all the properties of area, distance and angular conformity, within some acceptable limit. Examples of compromise projections are the Winkel Tripel projection and the Robinson projection (see figure_robinson_projection), which are often used for world maps.

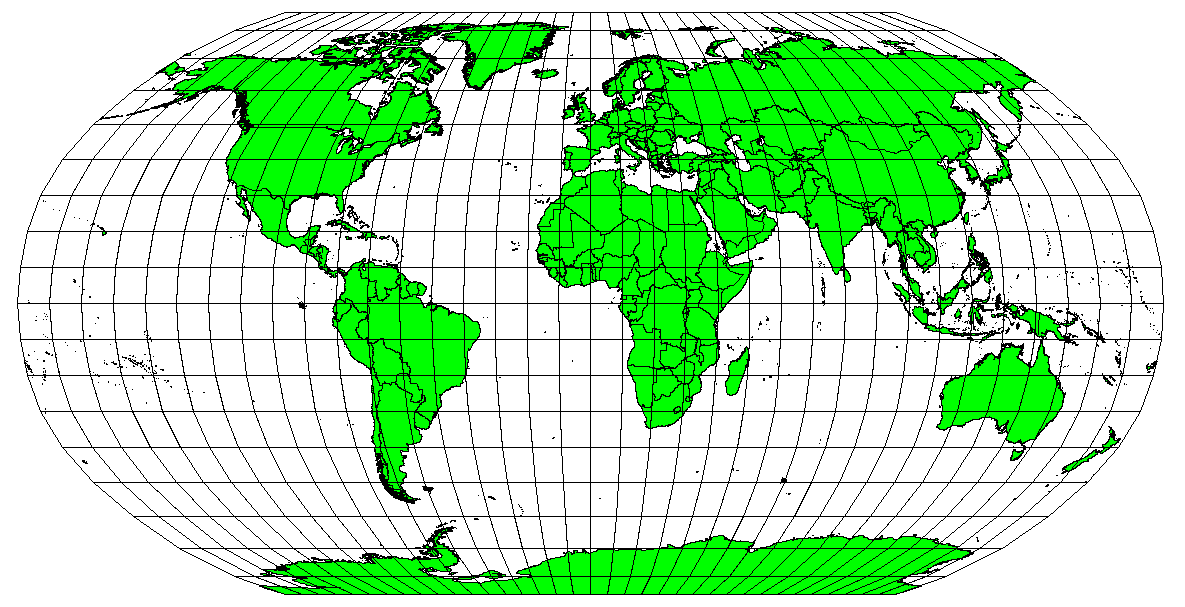
La proyección Robinson es un compromiso en el que la distorsión del área, la conformidad angular y la distancia son aceptables.

Generalmente es imposible preservar a la vez todas las propiedades en una proyección cartográfica. Esto significa que cuando se quieren realizar operaciones analíticas de precisión, es necesario utilizar una proyección de mapa que proporcione las mejores propiedades para dichos análisis. Por ejemplo, si se necesita medir distancias en el mapa, se debería tratar de usar una proyección cartográfica que proporcione alta precisión para las distancias.

Proyecciones cartográficas con conformidad angular¶

Cuando se trabaja con un globo, las principales direcciones de la rosa de los vientos (Norte, Este, Sur y Oeste) siempre estarán formando 90 grados entre sí. En otras palabras, el Este siempre se encontrará formando un ángulo de 90 grados con el Norte. En un mapa de proyección también es posible mantener unas propiedades angulares correctas. Un mapa cartográfico que mantiene esta propiedad de conformidad angular se denomina conformal o proyección ortomórfica

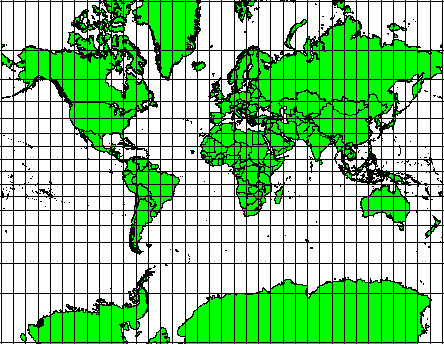
Estas proyecciones se utilizan cuando es importante preservar las relaciones angulares. Por lo general se utilizan en navegación y en meteorología. Es importante recordar que respetar los ángulos reales en un mapa es complicado para grandes áreas y que sólo se debe intentar para pequeñas porciones de tierra. Las proyecciones de tipo conformal dan como resultado distorsiones en las áreas, lo que significa que si la medida de áreas se realiza sobre el mapa, éstas serán incorrectas. Cuanto mayor es el área, menos precisa será su medida en el mapa. Ejemplos de este tipo de proyección son la de Mercator (como se muestra en la figura figure_mercator_projection) y la de Cónica Conformal de Lambert. El Servicio Geológico de los E.E.U.U., utiliza una proyección conformal para muchos de sus mapas.

La proyección Mercator, por ejemplo, se utiliza cuando las relaciones angulares son importantes, pero la relación de las áreas está distorsionada.

Proyecciones cartográficas con igual distancia¶

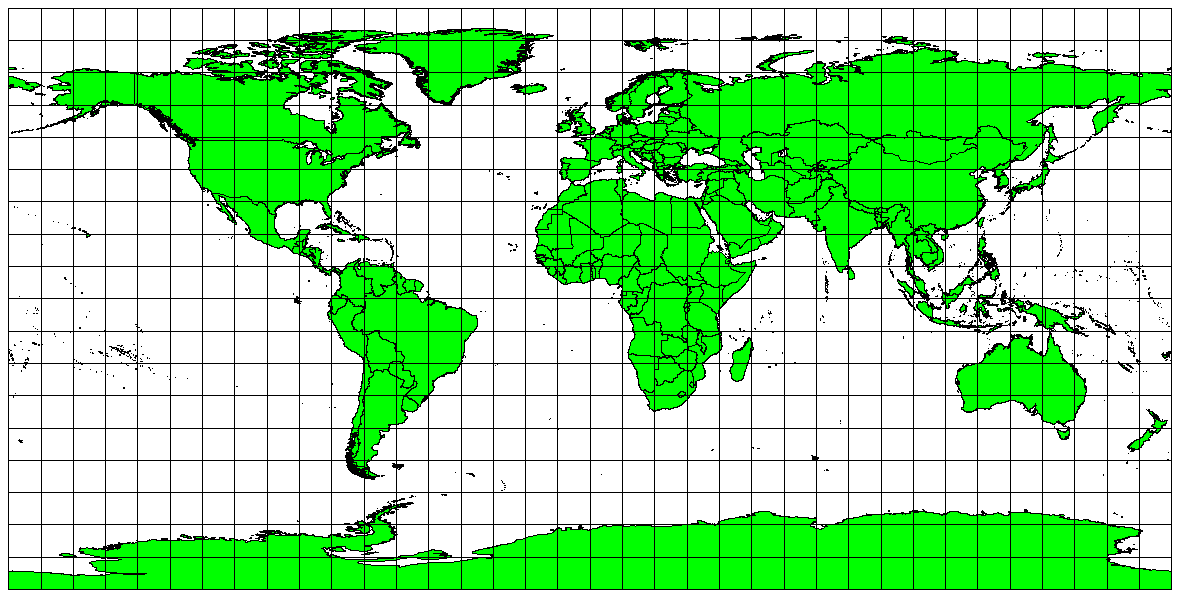
Si el objetivo de proyectar un plano es medir de forma precisa las distancias, se debería elegir una proyección que esté diseñada para preservar las mismas de manera adecuada. Dichas proyecciones, denominadas proyecciones equidistantes, requieren que la escala del mapa se mantenga constante. Un mapa se denomina equidistante cuando representa correctamente distancias dede el centro de la proyección o a lo largo de ciertas lineas. Este tipo de proyecciones se utiliza para mapas de radio, sismográficos y de navegación. La proyección Cilíndrica Equidistante de Plate Carreel (ver figure_plate_caree_projection) ya la Proyección Equirectangular son dos buenos ejemplos de proyecciones equidistantes. La Proyección Equidistante Acimutal es la utilizada en el emblema de las Naciones Unidas (ver figure_azimuthal_equidistant_projection).

La proyección Plate Carree Cilíndrica Equidistante, por ejemplo, se utiliza cuando la precisión en distancias es importante.

El Logo de las Naciones Unidas utiliza la Proyección Acimutal Equidistante.

Proyecciones con áreas iguales¶

When a map portrays areas over the entire map, so that all mapped areas have the same proportional relationship to the areas on the Earth that they represent, the map is an equal area map. In practice, general reference and educational maps most often require the use of equal area projections. As the name implies, these maps are best used when calculations of area are the dominant calculations you will perform. If, for example, you are trying to analyse a particular area in your town to find out whether it is large enough for a new shopping mall, equal area projections are the best choice. On the one hand, the larger the area you are analysing, the more precise your area measures will be, if you use an equal area projection rather than another type. On the other hand, an equal area projection results in** distortions of angular conformity** when dealing with large areas. Small areas will be far less prone to having their angles distorted when you use an equal area projection. Alber’s equal area, Lambert’s equal area and Mollweide Equal Area Cylindrical projections (shown in figure_mollweide_equal_area_projection) are types of equal area projections that are often encountered in GIS work.

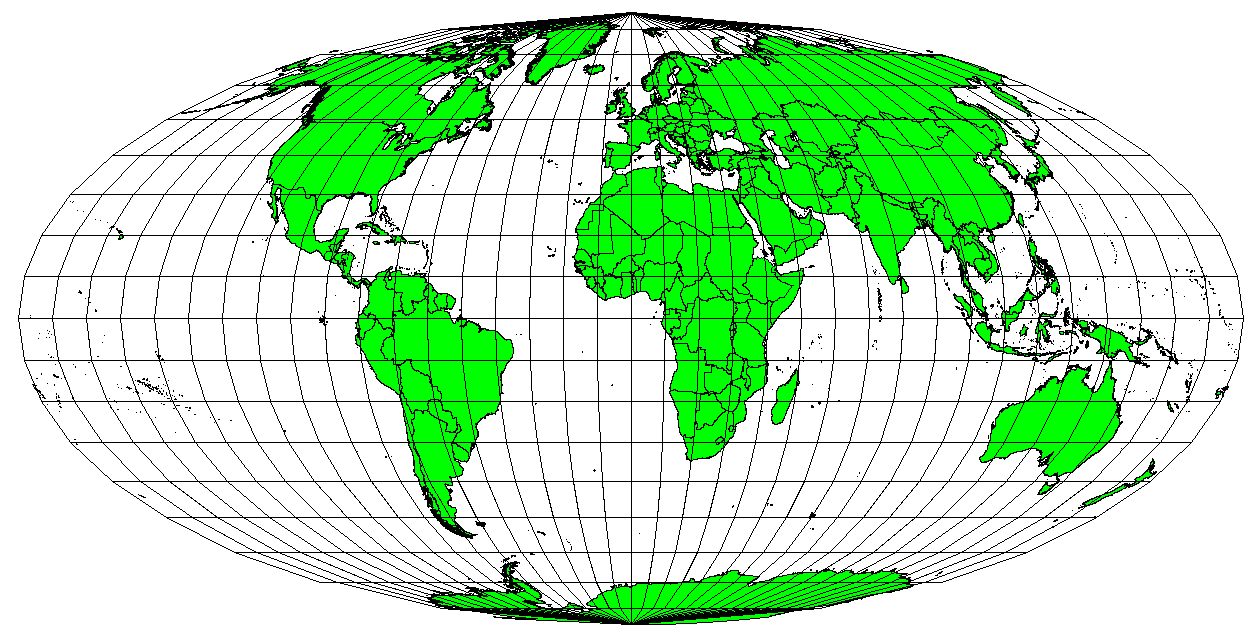
La proyección cilíndrica de igual área de Mollweide, por ejemplo, garantiza que todas las áreas en el mapa presentan la misma relación de proporcionalidad con dichas áreas en la Tierra.

Téngase en cuenta que el tema de las proyecciones cartográficas es muy complejo. Existen cientos de tipos diferentes de proyecciones y cada una intenta representar sobre el papel una porción del mundo de la forma más fidedigna posible. En realidad, la decisión de qué proyección utilizar, será a menudo una elección personal. La mayoría de los países utilizan unos métodos comunes de proyección que, al realizar intercambios de datos, seguirán la tendencia nacional

El Sistema de Referencia de Coordenadas (SRC) en detalle¶

Con la ayuda de Sistemas de Referencia de Coordenadas (SRC) cualquier punto de la tierra puede ser definido por tres números denominados coordenadas. En general, los SRC se pueden dividir en sistemas de referencia de coordenadas proyectados (también denominados Cartesianos o sistemas de referencia de coordenadas rectangulares) y sistemas de referencia de coordenadas geográficos.

Sistema de Coordenadas Geográficas¶

El uso de Sistemas de Referencia de Coordenadas geográficas es muy común. Utilizan los grados de latitud y longitud y en ocasiones un valor de altitud para definir la situación de un punto sobre la superficie terrestre. El sistema más popular se denomina WGS 84.

Las Líneas de latitud discurren paralelas al ecuador y dividen la tierra en 180 secciones equiespaciadas desde el Norte hasta el Sur (y viceversa). La línea de referencia para la latitud es el ecuador y cada hemisferio se divide en noventa secciones con cada una representando un grado de latitud. En el hemisferio norte, los grados de latitud se miden desde cero en el ecuador a noventa en el polo norte. Igualmente, en el hemisferio sur, los grados de latitud se miden desde cero en el ecuador hasta noventa en el polo sur. Para simplificar la digitalización de los mapas, los grados de latitud en el hemisferio sur reciben valores negativos (0 a -90º). Donde quiera que nos situemos sobre la superficie de la tierra, la distancia entre líneas de latitud es siempre la misma (60 millas naúticas). Vea la imagen figure_geographic_crs para obtener una representación gráfica.

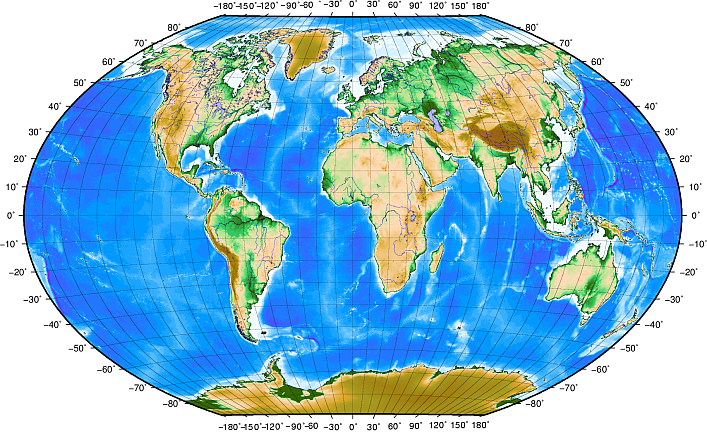
El Sistema de coordenadas geográficas con líneas de latitud paralela al ecuador y líneas de longitud con el primer meridiano a través de Greenwich.

Las Líneas de longitud, por otra parte no se ajustan tan bien al estándar de uniformidad. Éstas son perpendiculares al ecuador y convergen en los polos. La línea de referencia para la longitud (el meridiano cero) transcurre desde el polo Norte al polo Sur atravesando Greenwich, Inglaterra. A partir de ella, se definen nuevas líneas desde 0 a 180 grados al Este u Oeste del meridiano cero. Fíjese en cómo los valores al Oeste toman valores negativos al utilizarse en aplicaciones digitales de mapeado. Vease la imagen figure_geographic_crs.

En el ecuador, y sólo en el ecuador, la distancia representada por una línea de longitud y una de latitud es la misma. Conforme nos desplazamos hacia los polos, la distancia entre líneas de longitud va disminuyendo progresivamente hasta que, en el punto exacto de los polos, todas las líneas de longitud repartidas en los 360º se representan por un solo punto que se podría señalar con un dedo (probablemente preferirías llevar guantes). Cuando se utiliza el sistema de coordenadas de referencia, tenemos una red de líneas que dividen la tierra en cuadros que cubren, aproximadamente, 12363.365 kilómetros cuadrados en el acuador — un buen comienzo, pero no muy práctico a la hora de determinar la ubicación de cualquier cosa dentro de dicho cuadro.

Para ser realmente útiles, la red del mapa debe ser dividida en secciones suficientemente pequeñas de forma que puedan ser utilizadas para describir (con un nivel aceptable de precisión) la ubicación de un punto en el mapa. Para cumplir esto, los grados se dividen en minutos (') y segundos ("). Cada grado se compone de sesenta minutos y cada minuto en sesenta segundos (3600 segundos en un grado). Así que, en el ecuador, un segundo de latitud o longitud = 30.87624 metros.

Sistema de referencia de coordenadas proyectado¶

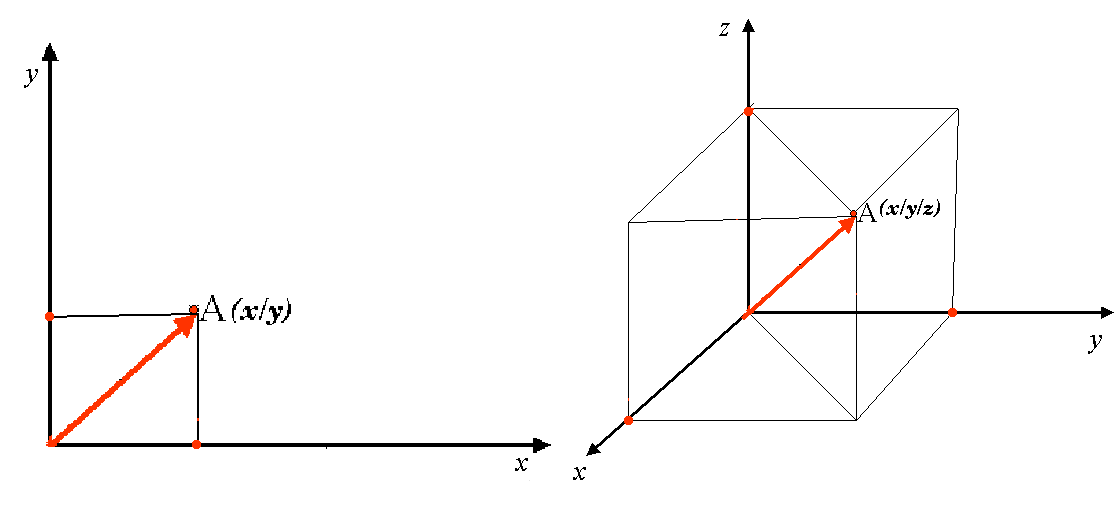
Un sistema de referencia de coordenadas bidimensional se define normalmente mediante dos ejes. Ubicados en ángulo recto uno respecto al otro, forman el denominado plano XY (vea la parte izquierda de figure_projected_crs). El eje horizontal se denomina generalmente X, y el eje vertical se denomina Y. En un sistema de referencia de coordendas tridimensioanl, se añade otro eje, generalmente denominado Z. Éste se coloca a su vez formando ángulo recto con los ejes X e Y. El eje Z proporciona la tercera dimensión del espacio (ver el lado derecho de figure_projected_crs). Cada punto expresado en coordenadas esféricas puede ser representado mediante una coordenada X Y Z.

Sistema de referencia de coordenadas de dos y tres dimensiones.

Por lo general, un sistema de referencia de coordenadas proyectadas en el hemisferio sur (al sur del ecuador), tiene su orígen en el ecuador a una Longitud específica. Esto significa que los valores de Y se incrementan hacia el Sur y los valores de X se incrementan hacia el Oeste. En el hemisferio norte (al norte del ecuador) el orígen es también el ecuador a una determinada Longitud. Sin embargo, ahora los valores de Y se incrementarán hacia el Norte y los de X lo harán hacia el Este. En la siguiente sección, describimos un sistema de referencia de coordenadas proyectadas, denominado Universal Transverse Mercator (UTM), utilizado a menudo para Sudáfrica.

El SRC Universal Transverse Mercator (UTM) en detalle¶

El sistema de referencia coordenadas Universal Transverse Mercator (UTM) tiene su orígen en el ecuador en una determinada Longitud. En él, los valores de Y crecen hacia el Sur y los valores de X lo hacen hacia el Oeste. El SCR UTM es un mapa cartográfico global. Esto significa que generalmente se usa en todo el planeta. Pero como se ha comentado más arriba en la sección ‘precisión de los mapas cartográficos’, cuanto mayor sea el área (por ejemplo, Sudáfrica) mayor será la distorsión angular, de distancia y área. Para evitar una distorsión excesiva, el mundo se divide en 60 zonas iguales correspondientes a 6 grados de anchura en la dirección Este-Oeste. Las zonas UTM se numeran desde 1 a 60, comenzando en la la línea internacional de cambio de fecha (zona 1 a 180 grados Oeste de longitud) y avanzando hacia el Este de nuevo hasta las línea internacional de cambio de fecha (zona 60 a 180 grados Este de longitud) como se muestra en figure_utm_zones.

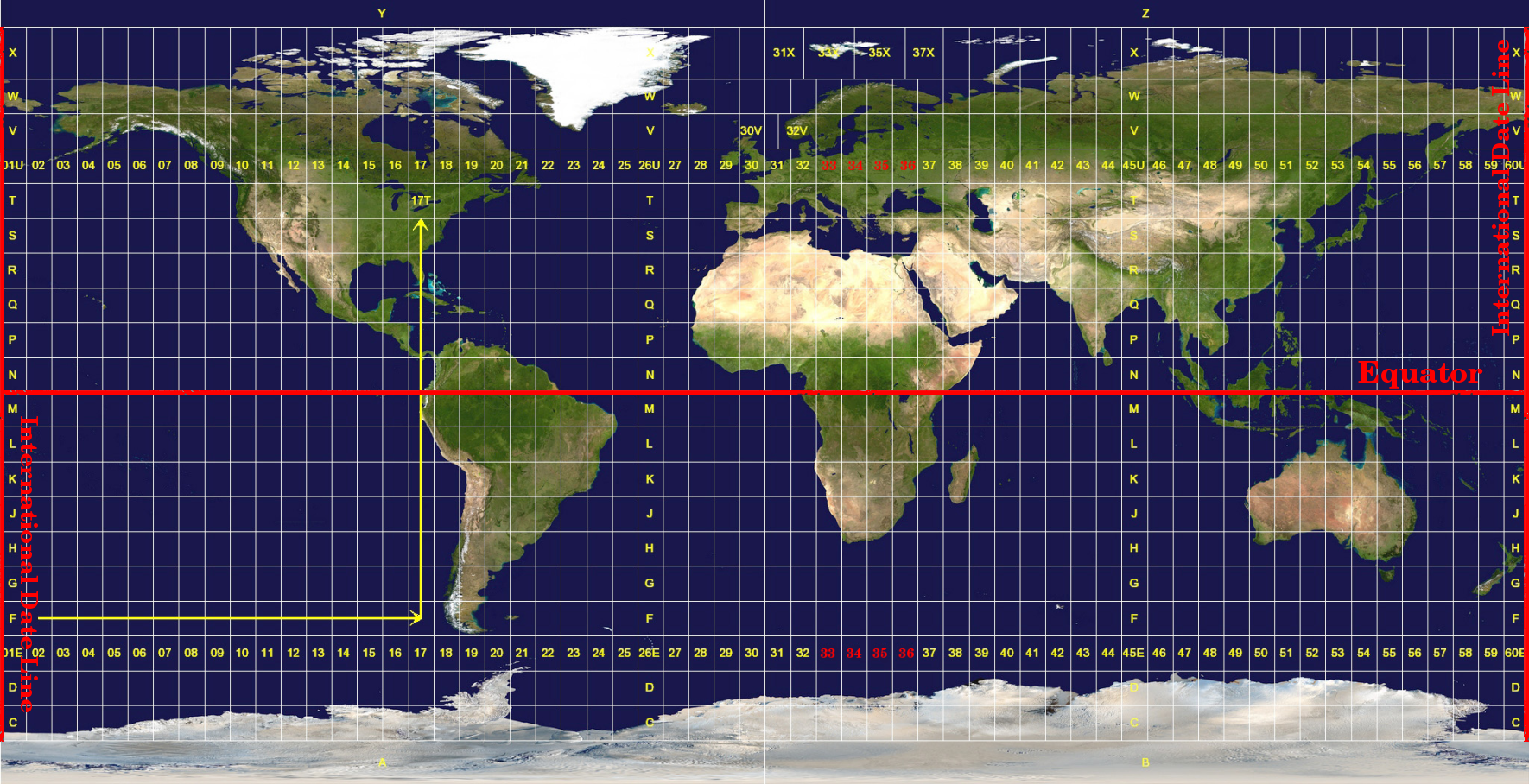
Las zonas de Universal Transverse Mercator. Para las zonas de Sudafrica se utilizan UTM 33S, 34S, 35S, y 36S.

Como se puede observar en figure_utm_zones y figure_utm_for_sa, Sudáfrica está cubierta por cuatro zonas UTM para minimizar la distorsión. Las zonas se denominan UTM 33S, UTM 34S, UTM 35S and UTM 36S. La letra S tras el número de zona indica que éstas están ubicadas al sur del ecuador.

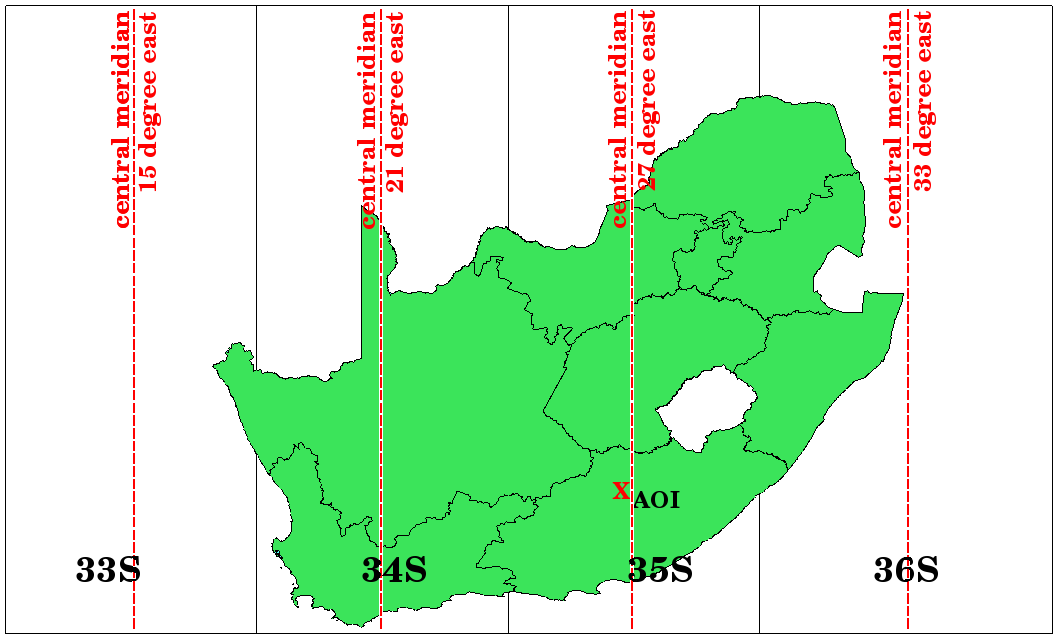
Las zonas UTM 33S, 34S, 35S y 36S son sus longitudes principales (meridianos) utilizadas para proyextar Sudáfrica con alta precisión. La cruz roja muestra un Área de Interés (AI).

Digamos, por ejemplo, que queremos definir una coordenada bidimensional dentro del Área de Interés (AI) marcada con una cruz roja en figure_utm_for_sa.. Se puede ver que, el área está localizada dentro del la zona UTM 35S. Esto significa que, para minimizar la distorsión y obtener unos resultados precisos de las medidas, deberíamos utilizar la zona UTM 35S como el sistema de coordenadas de referencia.

The position of a coordinate in UTM south of the equator must be indicated with the zone number (35) and with its northing (y) value and easting (x) value in meters. The northing value is the distance of the position from the equator in meters. The easting value is the distance from the central meridian (longitude) of the used UTM zone. For UTM zone 35S it is 27 degrees East as shown in figure_utm_for_sa. Furthermore, because we are south of the equator and negative values are not allowed in the UTM coordinate reference system, we have to add a so called false northing value of 10,000,000 m to the northing (y) value and a false easting value of 500,000 m to the easting (x) value. This sounds difficult, so, we will do an example that shows you how to find the correct UTM 35S coordinate for the Area of Interest.

Proyección al vuelo¶

Como podemos imaginar, se puede dar la situación en la que los datos que queramos utilizar en un SIG, estén proyectados en sistemas de coordenadas de referencia distintos. Por ejemplo, podríamos tener una capa vectorial que mostrase los límites de Sudáfrica proyectados en UTM 35S y otra capa vectorial con información sobre precipitación de lluvia en el sistema de coordenadas geográficas WGS 84. En el SIG, ambas capas se colocarán en lugares totalmente distintos dentro de la ventana al usar distintos sistemas de proyección.

Para solventar este problema, GIS incluye una funcionabilidad llamada proyeccion sobre vuelo esto significa que puedes**definir** una proyeccion certera cuando inicias el GIS y todas las capas que usted cargo, sin importar el sistema de coordenadas de referencias que tengan, seran automaticamente mostradas en la proyeccion que usted definio. Esta funcionabilidad le permirte cubrir las capas dentro de la ventana del mapa de su GIS, a pesar de que puedan estar en sistema de referencia diferente

Problemas comunes / cosas a tener en cuenta¶

El tema de los mapas cartográficos es muy complejo e incluso algunos profesionales que han estudiado geografía, geodesia u otras ciencias relacionadas con los SIG, a veces tienen problemas con la correcta definición de las proyecciones y los sistemas de coordenadas de referencia. A menudo, al trabajar con un SIG, los datos con los que trabajamos ya estarán proyectados. En la mayoría de los casos esos datos utilizarán un cierto SCR de forma que no será necesario crear un nuevo SCR o realizar conversiones a otro SCR. A pesar de esto, siempre es positivo tener una idea de los conceptos sobre los SCR y los mapas cartográficos.

¿Qué hemos aprendido?¶

Vamos a concluir lo que hemos cubierto en esta hoja de trabajo:

• Las Proyecciones cartográficas muestran la superficie de la tierra en dos dimensiones mediante una hoja de papel o una pantalla de ordenador.

• Hay proyecciones de mapa global, pero la mayoría de las proyecciones se crearon y optimizaron para proyectar áreas más pequeñas de la superficie de la tierra.

• Las proyecciones cartográficas no son representaciones absolutamente exactas de la Tierra esférica. Muestran distorsiones de conformidad angular, la distancia y la zona. Es imposible preservar todas estas características al mismo tiempo en una proyección cartográfica.

• Un Sistema de Referencia de Coordenadas (SRC) define, con la ayuda de coordenadas, cómo las dos dimensiones, el mapa proyectado se relaciona a ubicaciones reales de la tierra.

• Hay dos diferentes tipos de sistemas de referencia de coordenadas: Sistema de Coordenadas Geográfica y Sistema de Coordenadas Proyectada.

• Proyección Al vuelo es una funcionalidad en SIG que nos permite sobreponer capas,, incluso si estas son proyectadas en diferentes sistema de referencia de coordenadas.

Ahora inténtalo¶

Aqui estan algunas ideas para que intente con sus aprendizes:

• Inicie QGIS, cargue dos capas del mismo área pero con diferentes sistemas de proyección y pida a los alumnos que localicen varios puntos en las dos capas. Puede mostrarles que no es posible superponer ambas capas. Ahora elija Geographic/WGS 84 como el SCR en el diálogo Propiedades de Proyección y active la casilla Activar transformación SCR en tiempo real. Vuelva a cargar las mismas capas y deje que los alumnos comprueben como funciona la proyección en tiempo real.

• Puede abrir el diálogo Propiedades de Proyección en QGIS y enseñar a sus alumnos la gran variedad de Sistemas de Referencia de Coordenadas existentes, de forma que puedan hacerse una idea de la complejidad del tema tratado. Con la transformación de SRC en ‘tiempo real’ activada, se pueden seleccionar distintos SRC para mostrar la misma capa en diferentes sistemas.

Algo para pensar¶

If you don’t have a computer available, you can show your pupils the principles of the three map projection families. Get a globe and paper and demonstrate how cylindrical, conical and planar projections work in general. With the help of a transparency sheet you can draw a two-dimensional coordinate reference system showing X axes and Y axes. Then, let your pupils define coordinates (x and y values) for different places.

Lectura adicional¶

Libros

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

Sitios web

• http://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html
• http://geology.isu.edu/geostac/Field_Exercise/topomaps/index.htm

La Guia del Usuario QGIS tambien tiene mas informacion detallada de como trabajar con mapa de proyecciones en QGIS

¿Qué sigue?¶

En la seccion que sigues tomaremos una vista mas cerca de el Mapa de produccion