空間参照系¶

概要¶

地図投影法 は，紙やコンピュータの画面上に地球や地球の一部の表面を描画しようとします。 空間参照系 (CRS)は，座標によって，どのようにGISの中の投影された二次元が地球の実際の場所と関係づけられているかを決定します。どの投影法と空間参照系を使うかを決めるのは，しばしばデータの可用性やあなたが行いたい解析，あなたが仕事をしたい場所の地域の範囲によります。

地図投影法の詳細¶

地球の形を表現する従前の方法は，球体を使う方法です。しかしながら，この方法には問題があります。球体は地球の形状の大半を保持し，大陸の大きさという空間的特徴を表すが，ポケットにしまって持ち歩くのは大変難しい。それは，大変小さなスケール(例えば1:100,000,000)で使うときのみ便利です。

GISアプリケーションで一般に使われる大部分の主題地図データは，かなり大きいスケールです。典型的なGISデータセットは，1:250000かそれより大きいです。このサイズの球体は，製作するのが高価で難しく，持ち歩くのも困難です。このため，地図制作者は，球状の地球を二次元でかなり正確に表す**地図投影法**と呼ばれる技術を発展させてきた。

近距離で見ると、地球は比較的平坦に見えます。しかし、宇宙から見ると、地球は比較的球形であることがわかります。地図は、次の地図制作の話題の中で見られるように、現実の表現です。それらは、図形だけでなく、図形の形状と空間配置を表すように設計されています。各地図投影法には**長所**と**短所**があります。地図の最適な投影法は、地図の**縮尺**がどれほどで、それが使用される目的が何であるかによって変わります。たとえば、ある投影法は、アフリカ大陸全体の地図作成に使用すると許容範囲外の歪みが生じるが、自国内での**大縮尺（詳細）地図**には優れた選択肢となります。地図投影法の性質は、地図のデザイン面に何かしら影響する場合もあります。投影法は、小領域に適するものあれば、東西に大きく広がる地図領域に適するもの、南北に大きく広がる地図領域に適するものもあります。

地図投影法の大きな３つ¶

地図投影を作成するプロセスは、不透明な地形が配置された透明な地球の中に光源を配置することによって視覚化できます。次に、図形の外形線を2次元の平らな紙に投影します。球を**円筒**、円錐、または**平面**としても、さまざまな方法で投影できます。これらの方法のそれぞれは、地図投影族 と呼ばれるものを生成します。したがって、平面投影 の族、円柱投影 の族、円錐投影 の族があります（figure_projection_families_を参照）。

Figure Projection Families 1:

3つの地図投影の族。それらは）円筒投影、b）円錐投影、c）平面投影と表せます。

今日では、もちろん、平らな紙片に球状の地球を投影するプロセスは、幾何学と三角法という数学的原理を用いて行われます。これは、地球を通過する光の物理的な投影を再現します。

地図投影の精度¶

地図投影は、球形の地球の絶対的に正確な表現では決してありません。地図投影処理の結果として、すべての地図は**正角性、距離及び面積 における歪み**を示します。地図投影は、これらの特性のいくつか組み合わせることもありますし、またはいくつかの許容限界内で領域、距離および正角性のすべての性質を歪ませる妥協もあります。妥協の投影の例は**ヴィンケル投影（第 3 図法）**と**ロビンソン投影**（figure_robinson_projection_を参照）で、よく世界地図に使用されています。

Figure Robinson Projection 1:

ロビンソン投影エリア、角度整合と距離の歪みが許容される妥協点です。

地図投影で同時にすべての特性を維持するのは通常不可能です。これは、正確な分析操作を実行したい場合、分析のための最良の特性を与える地図投影を使用する必要があることを意味します。たとえば地図上で距離を計測する必要がある場合は、データに対して距離精度が高い地図投影を使用してみてください。

正角性を持つ地図投影¶

球で作業する場合、羅針図の主な方向（北、東、南、西）は常に相互に90度で発生します。言い換えれば、東は常に北へ90度の角度で発生します。正しい**角度性質**を維持することは地図投影上でも保存できます。正角性のこの性質を保持する地図投影は**コンフォーマル**または** orthomorphic投影と呼ばれます。

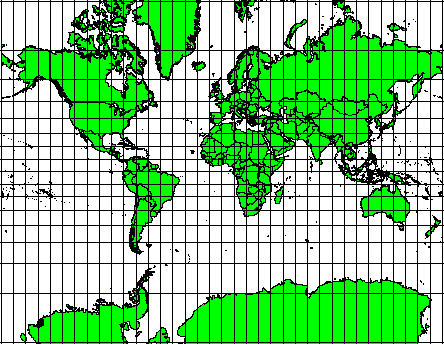
**角度関係の保存**が重要であるときはこれらの投影が使用されます。これらは一般に航行や気象の業務に使用されています。大きな領域では地図上の真の角度を維持することは困難であり、これは地球の小さな部分のためにだけ試みるべきことを覚えておくことが重要です。投影のコンフォーマルタイプは領域の歪みをもたらし、地図上での面積計測がなされる場合にそれらが不正確になるだろうことを意味します。領域が大きいほど面積計測の精度は低くなります。例は**メルカトル図法**（figure_mercator_projection_に示すように）と**ランベルト正角円錐図法です。米国地質調査所は、その地形図の多くでコンフォーマル投影を使用しています。

Figure Mercator Projection 1:

メルカトル図法は、例えば、角度関係が重要である場合に使用されるが、領域の関係が歪んでいます。

正しい距離での地図投影法¶

地図投影での目標が正確な距離を計測することである場合は、十分に距離を維持するように設計された投影を選択する必要があります。このような投影は**等距投影**と呼ばれ、地図の**縮尺**が**一定に保存**されることを必要とします。地図は、地図上の投影の中心から他の場所へ距離を正しく表すとき、等距です。**等距投影**は投影の中心からまたは所定の線に沿って、正確な距離を維持します。これらの投影は、ラジオや地震の図化のため、および航行に使用されています。**プレートカレ等距離円筒**（figure_plate_caree_projection_参照）**正距円筒図法**は、等距離射影の2つの良い例です。**正距方位図法**（figure_azimuthal_equidistant_projection_を参照）は国連の紋章に用いられる投影です。

Figure Plate Carree Projection 1:

正確な距離測定が重要であるときは、例えばプレートカレ等距円筒投影が使用されます。

Figure Azimuthal Equidistant Projection 1:

国際連合のロゴは正距方位図法が用いられています。

面積の正しい投影法¶

地図が 等積図 であるのは、地図化されたすべての面積が、それらが表す地球上の領域と同じ比例関係になるように、地図全体の領域を描写するときです。実際には、一般的な参照地図と教育地図では、ほとんどの場合、 等積投影法 を使用する必要があります。名前が示すように、これらの地図は、実行する計算の中で面積の計算が最も重要なときに最もよく使用されます。たとえば、町のある領域について新しいショッピングモールに十分な大きさがあるか調査する分析をしようとしている場合には、等積投影法が最適です。分析している領域が広くなるほど、別のタイプではなく等積投影法を使用するときにより正確な面積測定値が得られます。その一方で、等積投影法は、広い領域を扱うときは**正角性における歪み**をもたらします。等積投影法を使用するとき、小さな領域では角度が歪む傾向は大幅に減ります。 アルベール等積 ランベルト等積 モルワイデ等積円筒投影法 （figure_mollweide_equal_area_projection_に示されている）は、GIS作業でよく見かける等積投影のタイプです。

Figure Mollweide Equal Area Projection 1:

モルワイデ等積円筒投影は、例えば、地図化された領域はすべて、地球上の領域に同一の比例関係を有していることを保証します。

地図投影は非常に複雑なトピックであることに留意してください。世界的な利用可能な異なる投影法は何百もあり、それぞれが紙の平らな部分にできるだけ忠実に地球の表面の特定の部分を描写しようとします。実際にどの投影を使用するかの選択は多くの場合、あなたのためになされます。ほとんどの国には一般的に使用される投影があり、人々はデータを交換するとき **全国的傾向**に従います。

空間参照系(CRS)の詳細¶

座標系（CRS）の助けを借りて、地球上のあらゆる場所では、座標と呼ばれる3つの数字のセットで指定できます。一般にCRSは**投影座標系に（デカルト又は直角座標系とも呼ばれる）と**地理座標系**にに分類できます。

地理参照系¶

地理座標参照系を使用することは非常に一般的です。彼らは、地球の表面上の位置を記述するために緯度と経度と時には高さ値の程度を使用しています。最も人気のある**はWGS 84 **と呼ばれています。

**緯線**は赤道に平行に走り、北から南（または南から北へ）の180等分されたセクションに地球を分割します。緯度の基準線は赤道であり、各**半球**は緯度1度を表す90のセクションに分割されています。北半球では、緯度は赤道の0度から北極の90度までで測定されます。南半球では、緯度は赤道の0度から南極の90度までで測定されます。地図のデジタル化を簡素化するために、南半球の緯度度には負の値（0〜-90°）が割り当てられることがよくあります。地球のどこにいても、緯線間の距離は同じです（60海里）。絵画的な図はfigure_geographic_crs_を参照してください。

Figure Geographic CRS 1:

緯線は赤道に平行で、経線は本初子午線がグリニッジを通る地理座標系。

一方**経線**は均一性の標準に非常によく立っていません。経線は赤道に垂直に引かれ両極に収束します。経度のための基準線（本初子午線）は、イングランドのグリニッジを通って北極から南極まで引かれます。続く経線は本初子午線の東または西にゼロから180°で測定されます。本初子午線の西値は、デジタルマッピングアプリケーションで使用するために負の値が割り当てられます。絵ビュー用figure_geographic_crs_を参照してください。

赤道で、そして赤道のみで、経度の線で表される距離は緯度1度で表される距離に等しくなります。極の方に移動するにつれ経線間の距離は徐々に小さくなっていき、ちょうど極の位置になると経度の全ての360°は単一の点で表現され、上に指を置くことができるでしょう（手袋を着用したくなるでしょうが ）。地理座標系を使用すると、赤道では約12363.365平方キロメートルを覆う正方形に地球を分割する線格子を得られます、—手始めには良いですがその正方形内の何かの位置を決定するために非常に有用ではありません。

真に有用であるためには、地図の格子は、（精度の許容レベルで）地図上の点の位置を記述するために使用できるように、十分小さな部分に分割されなければなりません。これを達成するために、度は**分 **（ `` ‘ ``）と**秒**（ `` “` `）に分割されます。1度は60分、1分は60秒です（1度は3600秒）。したがって、赤道では、緯度または経度の１秒＝ 30.87624メートルです。

基準座標系に投影¶

二次元座標参照系は、一般的に二つの軸によって定義されます。それらは互いに直角に、いわゆる XY平面 （左側のfigure_projected_crs_参照）を形成します。普通は横軸が X で縦軸が Y でラベルされています。三次元座標参照系においては、普通 Z でラベルされる別の軸が追加されます。この軸も X と Y 軸に対して直角です。 Z 軸は、空間の三次元（右側figure_projected_crs_参照）を提供します。球座標で表現されるすべての点は X　Y　Z 座標として表現できます。

Figure Projected CRS 1:

二及び三次元基準座標系。

南半球（赤道南）での投影座標参照系は通常、特定の**経度**で赤道にその原点を有しています。これは、Y-値は南に増加し、X-値は西に増加することを意味します。北半球（赤道北）でも、原点は特定の**経度**での赤道です。しかし今度は、Y値は北に増加し、X-値は東に増加します。次のセクションではしばしば南アフリカについて使用されるユニバーサル横メルカトル（UTM）と呼ばれる投影座標参照系を記載しています。

ユニバーサル横メルカトル（UTM）CRS詳細¶

ユニバーサル横メルカトル（UTM）座標系は、特定 経度 での 赤道 にその原点があります。今、Y値は南に増加し、X値は西に増加します。UTM CRSは、グローバル地図投影です。これは、それが一般的に世界中で使用されている、と意味します。しかし、既に上の「地図投影の精度」セクションに記載したように、領域が大きくなる（例えば、南アフリカ）ほど、角合わせ、距離、面積でより大きな歪みが発生します。大きすぎる歪みを回避するために、世界は東から西へ経度幅 6度 の 60の等しいゾーン に分割されています。** UTMゾーン** には国際日付線から始まる ** 1〜60** の番号が付けられていて（ ゾーン1 は西経180度）、 国際日付線 に戻るまで東へと進みます（ ゾーン60 は東経180度）figure_utm_zones_に示すように。

Figure UTM Zones 1:

ユニバーサル横メルカトルゾーン。南アフリカのためにUTMゾーン33S、34S、35S、36Sとが使用されています。

figure_utm_zones_とfigure_utm_for_sa_に見られるように、南アフリカは、歪みを最小限に抑えるために4つの ** UTMゾーン** で覆われています。 ゾーン は UTM 33S ** 、 **UTM 34S 、 UTM 35S と UTM 36S と呼ばれています。ゾーンの後の S はそのUTMゾーンが 赤道の南 に位置することを意味します。

Figure UTM for South Africa 1:

UTMゾーンは、その中央経度（経絡）と33S、34S、35S、36Sとは、高い精度で南アフリカを投影するために使用されます。赤の十字は関心領域（AOI）を示します。

例えば、figure_utm_for_sa_に赤い十字の付いた 関心領域（AOI） 内の二次元の座標を定義したいとします。領域が ** UTMゾーン35S**内に位置していることを、見ることができます。これが意味することは、歪みを最小限に抑え、正確な分析結果を得るために、座標系として ** UTMゾーン35S** を使用する必要があることです。

赤道南のUTM座標の位置はメートルで ゾーン番号 （35）とその 北距（y）値 と 東距（x）値 で示されなければなりません。 北距値 は 赤道 からの位置のメートルでの距離です。東距値**は使用されるUTMゾーンの **中央子午線**（経度）からの距離です。figure_utm_for_sa_に示すように、UTMゾーン35Sの場合、それは **東 27度 です。さらに、基準座標系UTMでは赤道南で負の値の使用することは許されないので、いわゆる**偽北距値**千万メートルを北距（Y）値に追加し、偽東距値500,000 mを東距（x）値に追加する必要があります。これは難しく聞こえますので、ここで 関心領域 に対する正しい UTM 35S 座標を見つける方法を示す例を出します。

オンザフライ投影¶

おそらく想像できるでしょうが、GISで使用するデータが異なる座標参照系に投影されている状況はありえます。たとえば、UTM 35Sで投影された南アフリカの国境を示すベクトルレイヤーと、WGS 84地理座標系で与えられた降雨に関する地点情報のベクトルレイヤーがあるとします。GISではこれら2つのベクトルレイヤーは、投影が異なるので、マップウィンドウ中で全く異なる領域に配置されます。

この問題を解決するために、多くのGISでは **オンザフライ**投影と呼ばれる機能が含まれています。つまり、GISを開始したときに特定の投影法を**定義**できます。また、ロードしたすべてのレイヤーは、座標系がどのようなものであっても、定義した投影法で自動的に表示されます。この機能は、GISの地図ウィンドウ内で**異なる**参照システムにあるかもしれないレイヤーを重ねることを可能にします。

一般的な問題 / 注意すべき点¶

トピック**地図投影**は非常に複雑であり、地理、測量、あるいはその他のGIS関連科学を研究している専門家ですら地図投影と基準座標系を正しく定義できないことがよくあります。GISで作業するときは通常、開始するデータをすでに投影しています。ほとんどの場合、これらのデータは、特定のCRSに投影されますので、新しいCRSを作成したり、そのデータをある CRSから別のCRSへ再投影する必要はありません。ですが、地図投影とCRSが意味することについて理解があるといつでも役に立ちます。

何を学びましたか？¶

このワークシートに覆われたものを包んでみましょう：

• 地図投影 は紙またはコンピュータ画面の二次元の平面部分に地球の表面を描きます。

• 全世界的な地図投影はありますが、ほとんどの地図投影は地球の表面の**小領域を投影するのに最適** なように作成されています。

• 地図投影では、球形の地球を絶対的に正確な表現することは決してありません。それらは**正角性、距離および面積における歪み** を示します。地図投影ですべてのこれらの特性を同時に保つことは不可能です。

• A Coordinate reference system (CRS) defines, with the help of coordinates, how the two-dimensional, projected map is related to real locations on the earth.

• 異なる２つの空間参照系があります。地理座標系 と**投影座標系** です。

• オンザフライ 投影は，別の空間参照系で投影されているレイヤーを重ねることを可能にするGISの機能です。

やってみよう¶

ここでは人に教える際のアイデアいくつか述べていきます:

• QGISを起動し、同じ領域で投影が異なる2つのレイヤーをロードして、生徒たちに2つのレイヤー上でいくつかの場所の座標を見つけさせましょう。二つのレイヤーをオーバーレイすることは不可能であることを示せます。その後、プロジェクトのプロパティ ダイアログの中で地理/ WGS 84などの座標系を定義し、チェックボックス|チェックボックス|　オンザフライCRS変換 を有効にします。同じ領域の二つのレイヤーを再度ロードし、生徒たちにオンザフライ投影がどのように機能するかを見せます。

• QGISで:guilabel:プロジェクトProperties ダイアログを開き、生徒たちがこのトピックが複雑であること理解するように多くの異なった座標系を見せる　ことができます。「オンザフライ」CRS変換が有効であると、同一のレイヤーを違った投影で表示するように違ったCRSを選択できます。

考えてみよう¶

利用できるコンピュータがない場合は、3つの地図投影の族の原則を生徒たちに見せることができます。球体と紙を取得し、円筒、円錐、平面の投影が一般的にどのように機能するかを示します。透明シートの助けを借りると、X軸とY軸を示す2次元の座標参照系を描くことができます。次に、生徒たちに異なる場所の座標（xとyの値）を定義させましょう。

より詳しく知りたい場合は¶

図書:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

ウェブサイト:

• http://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html
• http://geology.isu.edu/geostac/Field_Exercise/topomaps/index.htm

QGISユーザーガイドでは,地図投影法の操作についてより詳細な情報が含まれています.

次は?¶

このセクションでは私たちが**地図投影法**について詳しく見ていくのを援助します。