Koordinatenbezugssysteme

	Ziele:	Verstehen von Koordinatenbezugssystemen.
	Schlüsselwörter:	Koordinatenbezugssysteme (KBS), Kartenprojektion, On-The-Fly-Projektion, Breitengrad, Längengrad, Hochwert, Rechtswert

Übersicht

Kartenprojektionen versuchen die Erdoberfläche auf einem flachem Papier oder dem Bildschirm darzustellen. In einfachen Worten versuchen sie die Kugeloberfläche der Erde (3D) auf eine plane Form (2D) zu transformieren, so dass daraus eine plane Karte erstellt werden kann.

Ein Koordinatenbezugssystem (KBS) bestimmt mit Hilfe von Koordinaten den Bezug der zwei-dimensionalen projizierten Karte im GIS zu realen Orten an der Erdoberfläche. Die Entscheidung für die Nutzung einer Kartenprojektion und eines Koordinatenbezugssystems hängt von der räumlichen Ausdehnung des Arbeitsgebietes, der Art der geplanten Analyse und oft von der Verfügbarkeit der Daten ab.

Kartenprojektion im Detail

Eine traditionelle Methode zur Darstellung der Erdform ist die Nutzung von Globen. Dennoch gibt es ein Problem mit dieser Methode. Obwohl Globen den größten Teil der Erdform widerspiegeln und die räumliche Struktur der kontinent-großen Bestandteile darstellen, lassen sie sich nur sehr schwierig in der Tasche tragen. Außerdem sind sie nur für sehr kleine Maßstäbe (z.B. 1:100 Millionen) geeignet.

Die meisten thematischen Kartendaten, die in GIS-Anwendungen verwendet werden, haben bedeutend größere Maßstäbe. Typische GIS-Datensätze besitzen Maßstäbe von 1:250.000 oder größer, je nach Detailgrad. Ein Globus dieser Größe wäre sehr schwierig und teuer zu produzieren und noch schwieriger zu transportieren. Deshalb haben Kartografen eine Reihe von Techniken entwickelt namens Kartenprojektionen, die - mit angemesserer Genauigkeit - die kugelförmige Erde in zwei Dimensionen darstellen.

Von nahem betrachtet wirkt die Erde relativ flach. Aber vom Weltall aus sieht man, dass die Erde relativ kugelförmig ist. Wie wir im nächsten Thema Kartenherstellung sehen werden, sind Karten eine Widerspiegelung der Realität. Sie werden nicht nur entworfen, um Eigenschaften darzustellen, sondern auch Gestalt und räumliche Anordnung. Jede Kartenprojektion hat Vorteile und Nachteile. Die beste Kartenprojektion ist abhängig vom Maßstab der Karte und vom Verwendungszweck. Zum Beispiel könnte eine Karte inakzeptable Verzerrungen aufweisen, wenn sie für die Darstellung des gesamten afrikanischen Kontinents genutzt wird, könnte aber eine exzellente Wahl sein für eine großmaßstäbliche (detailiierte) Karte Ihres Landes. Die Eigenschaften einer Kartenprojektion können auch einige Konstruktionsmerkmale der Karte beeinflussen. Einige Projektionen sind geeignet für kleine Flächen, während andere ideal sind für Kartiergebiete mit großer Ost-West-Ausdehnung oder wieder andere für Kartiergebiete mit großer Nord-Süd-Erstreckung.

Die drei Familien der Kartenprojektionen

Der Prozess der Erstellung von Kartenprojektionen lässt sich am besten mit einer Lichtquelle vergleichen, die in einem durchsichtigen Globus positioniert wird und undurchsichtige Objekte auf seiner Oberfläche beleuchtet. Die Umrisse der Objekte werden dann auf ein zwei-dimensionales ebenes Stück Papier übertragen. Unterschiedliche Arten der Projektion können durch das Auflegen des Papiers auf den Globus in zylindrischer, kegelförmiger oder flacher Art und Weise erreicht werden. Jede dieser Methoden produziert eine sogenannte Familie von Kartenprojektionen. Es gibt die Familie der ebenen Projektionen, der zylindrischen Projektionen und der Kegelprojektionen (siehe figure_projection_families)

Die drei Kategorien von Kartenprojektionen. a) Zylinderprojektion, b) Kegelprojektion und c) Azimuthalprojektion.

Natürlich wird heutzutage der Prozess, die Erdkugel auf ein flaches Blatt Papier zu projizieren, unter Zuhilfenahme mathematischer Prinzipien aus der Geometrie und Trigonometrie durchgeführt. Dies stellt die physische Projektion von Lichtstrahlen durch den Globus nach.

Genauigkeit von Kartenprojektionen

Kartenprojektionen sind niemals eine exakte Übertragung der kugelförmigen Erdoberfläche. Durch den Prozess der Projektion zeigt jede Karte Verzerrungen bei Winkeln, Abständen und Flächen. Eine Kartenprojektion kann einige dieser Eigenschaften kombinieren oder sie stellt einen Mittelweg dar, der die Verzerrung von Flächen, Abständen und Winkeln in einem akzeptablen Rahmen hält. Beispiele für Projektionen die solch einen Mittelweg gehen sind die Winkel-Tripel-Projection und die Robinson Projektion (siehe figure_robinson_projection), die oft zur Herstellung und Visualisierung von Weltkarten genutzt werden.

Die Robinson Projektion ist ein Kompromiss, bei welchem Verzerrungen der Fläche, Winkeltreue und Distanz im Durchschnitt akzeptabel sind.

Es ist in der Regel nicht möglich, alle gewünschten Eigenschaften einer Kartenprojektion gleichzeitig zu erreichen. Wenn Operationen mit einer hohen Genauigkeit ausgeführt werden sollen, muss eine Kartenprojektion verwendet werden, die die besten Ergebnisse für diese Operation liefert. Wenn z. B. Abstände in der Karte gemessen werden sollen, sollte man eine Kartenprojektion mit hoher Längengenauigkeit verwenden.

Winkeltreue Kartenprojektionen

Wenn man mit einem Globus arbeitet, liegen die Hauptrichtungen des Kompasses (Nord, Ost, Süd und West) immer in einem Winkel von 90 Grad zueinander. Das bedeutet, dass Ost immer in einem Winkel von 90 Grad zu Nord liegt. Die Beibehaltung der korrekten Winkel kann auch mit einer Kartenprojektion erreicht werden. Eine Kartenprojektion die die Winkel richtig abbildet wird konforme Abbildung oder winkeltreue Abbildung genannt.

Diese Projektionen werden verwendet, wenn die Beibehaltung von Winkelbeziehungen wichtig ist. Sie werden in der Regel für Navigationsanwendungen oder in der Metorologie verwendet. Es ist wichtig zu beachten, dass die Beibehaltung von Winkelbeziehungen auf einer Karte für große Gebiete schwierig ist und daher eher für kleinere Gebiete der Erde verwendet werden sollte. Die winkeltreuen Abbildungen resultieren in einer Verzerrung von Flächen, d.h. Flächenmessungen in der Karte werden abweichende Ergebnisse liefern. Je größer die Flächen sind, desto größer werden die Abweichungen zur tatsächlichen Flächengröße ausfallen. Beispiele sind die Mercator-Projection (zu sehen in der Abbildung figure_mercator_projection) und die Lambert winkeltreue Kegelprojektion. Der U.S. Geological Survey nutzt für viele seiner topographischen Karten eine winkeltreue Projektion.

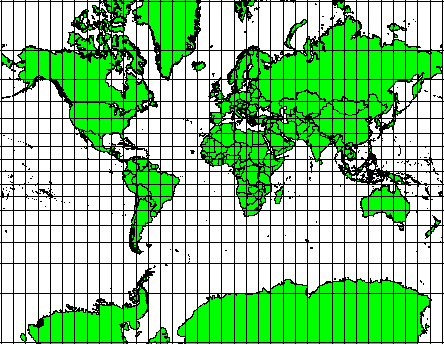
Die Mercator Projektion wird beispielsweise benutzt, wenn Winkeltreue wichtig ist, aber Flächen verzerrt dargestellt werden dürfen.

Längentreue Kartenprojektionen

Wenn das Ziel einer Kartenprojektion in der korrekten Messung von Abständen besteht, sollte man eine Projektion wählen, die Längen möglichst gut bewahrt. Solche Projektionen werden längentreue Projektionen genannt. Sie erfordern, dass die Größenverhältnisse in der Karte konstant gehalten werden. Eine Karte ist längentreu, wenn Abstände vom Zentrum der Projektion zu jedem beliebigen Punkt in der Karte korrekt wiedergegeben werden. Längentreue Projektionen behalten die korrekten Abstände entlang von gegebenen Linien aus dem Zentrum der Projektion bei. Diese Projektionen werden für die Kartierung von Radiowellen oder seismischen Wellen und für die Navigation verwendet. Die Plate-Carree-Projektion (siehe Abbildung figure_plate_caree_projection) und die äquirektanguläre Projektion sind zwei gute Beispiele von längentreuen Projektionen. Die Mittabstandstreue Azimutalprojektion wird für das Emblem der Vereinten Nationen verwendet (siehe figure_azimuthal_equidistant_projection).

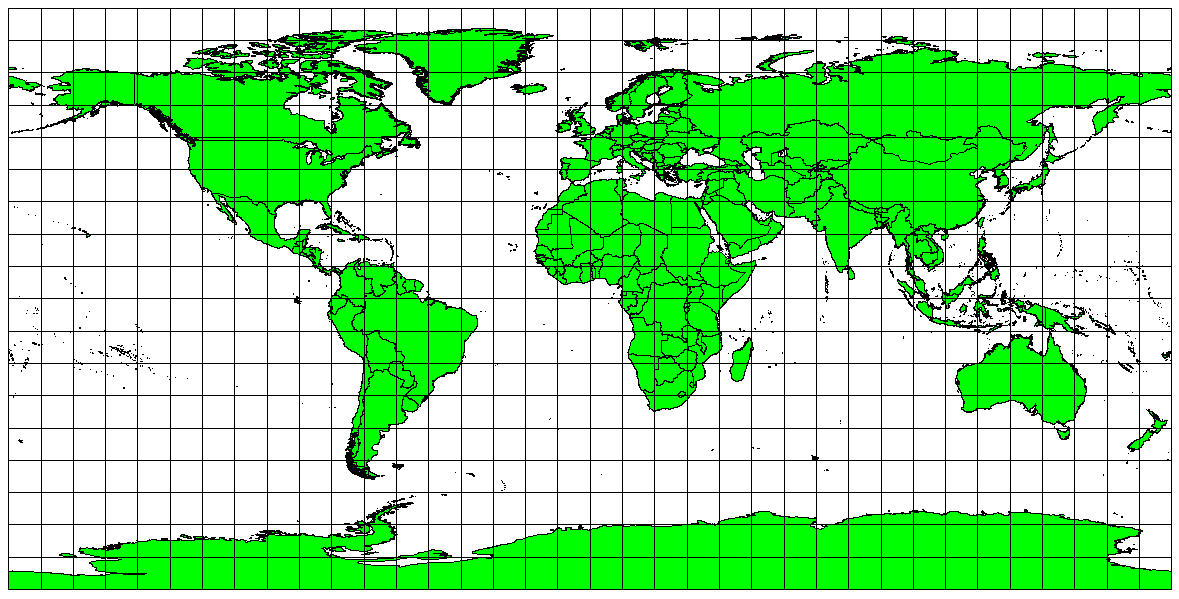
Die Plate-Carree-Projektion wird z.B. verwendet, wenn eine genaue Längenmessung wichtig ist.

Das Logo der Vereinten Nationen (UN) benutzt eine azimutale äquidistante Projektion.

Flächentreue Projektionen

Wenn Flächen in allen Bereichen einer Karte in demselben Verhältnis zur Fläche auf der Erdoberfläche stehen, dann handelt es sich um eine flächentreue Karte. In der Praxis erfordern allgemeine Karten oder Karten zu Lehrzwecken oft flächentreue Projektionen. Wie der Name es andeutet, sind diese Projektionen am besten geeignet, wenn vor allem Flächenberechnungen ausgeführt werden. Wenn man z.B. Flächen in der Stadt danach untersucht, ob sie die erforderliche Größe für ein Shoppingcenter haben, sind flächentreue Projektionen am besten geeignet. Je größer die untersuchten Flächen sind, desto genauer arbeiten flächentreue Projektionen gegenüber anderen Projektionen. Auf der anderen Seite führen flächentreue Projektionen bei der Arbeit mit großen Flächen zu einer Verzerrung der Winkelkonformität. Bei kleinen Gebieten fällt die Verzerrung von Winkeln bei Verwendung einer flächentreuen Projektion nicht so sehr ins Gewicht. Die Albers-Kegelprojektion, die Lambertsche Azimutalprojektion und die Mollweide-Projektion (gezeigt in der Abbildung figure_mollweide_equal_area_projection) sind Typen von flächentreuen Projektionen die oft in der Arbeit mit GIS anzutreffen sind.

Die Mollweide-Projektion stellt z.B. sicher, dass alle in der Karte dargstellten Flächen im selben Verhältnis zur zugehörigen Fläche auf der Erdoberfläche stehen.

Bedenken Sie, dass Kartenprojektion ein sehr komplexes Themengebiet ist. Es gibt hunderte verschiedener Projektionen weltweit, wobei jede versucht, einen bestimmten Teil der Erdoberfläche möglichst getreu auf einem ebenen Blatt Papier abzubilden. In der Realität wird einem die Wahl der Projektion oft abgenommen. In den meisten Ländern sind bestimmte Projektionen weit verbreitet. Beim Datenaustausch folgen die Leute in der Regel diesem nationalen Trend.

Koordinatenbezugssystem (KBS) im Detail

Mit Hilfe von Koordinatenbezugssystemen (KBS) kann jeder Ort auf der Erde durch eine Gruppe von drei Zahlen, genannt Koordinaten, beschrieben werden. Im Allgemeinen können KBS in projizierte Koordinatenbezugssysteme (auch kartesische oder rechtwinklige Koordinatenbezugssysteme genannt) und geographische Koordinatenbezugssysteme unterteilt werden.

Geografisches Koordinatensystem

Die Nutzung von geographischen Koordinatenbezugssystemen ist weit verbreitet. Sie verwenden Breiten- und Längengrade und manchmal Höhenwerte, um die Lage auf der Erdoberfläche zu beschreiben. Das beliebteste nennt sich WGS 84.

Breitengrade laufen parallel zum Äquator und teilen die Erde in 180 gleich weit entfernte Abschnitte von Nord nach Süd (oder von Süd nach Nord). Die Referenzlinie für die geographische Breite ist der Äquator und jede Erdhalbkugel ist in neunzig Abschnitte geteilt. Jeder Abschnitt entspricht einem Breitengrad. Auf der Nordhalbkugel werden die Breitengrade von null am Äquator bis 90 am Nordpol bemessen. Auf der Südhalbkugel werden die Breitengrade von 0 am Äquator bis 90 am Südpol bemessen. Um die Handhabung in Karten zu vereinfachen, erhalten die Breitengrade auf der Südhalbkugel oft negative Vorzeichen (0 bis -90°). An der Erdoberfläche ist die Distanz zwischen zwei Breitengraden immer identisch (60 nautische Meilen). Die Abbildung figure_geographic_crs stellt dies grafisch dar.

Das geographische Koordinatenenbezugssystem mit Linien der Breitengrade, die parallel zum Äquator verlaufen und Linien der Längengrade und dem Hauptmeridian durch Greenwich.

Längengrade verhalten sich dagegen nicht so einheitlich. Sie verlaufen lotrecht auf dem Äquator und konvergieren an den Polen. Die Referenzlinie für Längengrade (Hauptmeridian) verläuft vom Nordpol zum Südpol durch Greenwich in England. Die folgenden Längengrade werden von null bis 180 Grad in Ost- und Westrichtung ausgehend vom Hauptmeridian bemessen. In digitalen Karten werden für Längengrade westlich des Hauptmeridians negative Werte verwendet. Die Abbildung figure_geographic_crs stellt dies grafisch dar.

Nur am Äquator ist der Abstand zwischen zwei Längengraden gleich dem Abstand zwischen zwei Breitengraden. Wenn man sich in Richtung der Pole bewegt, wird der Abstand zwischen den Längengraden immer kleiner. An den Polen werden alle 360° Längengrade durch einen Punkt repräsentiert auf den man seinen Finger halten kann (man sollte dazu aber lieber Handschuhe anziehen). Das geographische Koordinatenbezugssystem unterteilt die Erdoberfläche in ein Gitter aus Vierecken, die am Äquator in etwa eine Fläche von 12363,365 Quadratkilometern erreichen. Ein guter Anfang, aber nicht ausreichend genau, um die Lage eines Objektes innerhalb solch eines Vierecks anzugeben.

Um wirklich nützlich zu sein, muss das Gitter weiter unterteilt werden, um damit die Lage eines Punktes auf der Karte (mit einer akzeptablen Genauigkeit) zu beschreiben. Um das zu erreichen, wird die Angabe Grad weiter unterteilt in Minuten (') und Sekunden ("). Es gibt sechzig Minuten in einem Grad und sechzig Sekunden in einer Minute (3600 Sekunden in einem Grad). Das bedeutet, dass am Äquator eine Längen- oder Breitensekunde einer Strecke von 30,87624 Metern entspricht.

Projizierte Koordinatenreferenzsysteme

Ein zweidimensionales Koordinatenbezugssystem ist normalerweise durch zwei Achsen definiert. In einem rechten Winkel zueinander bilden sie die sogenannte XY-Ebene (siehe figure_projected_crs auf der linken Seite). Die horizontale Achse wird in der Regel mit X und die vertikale Achse mit Y bezeichnet. In einem dreidimensionalen Koordinatenbezugssystem kommt eine weitere Achse, in der Regel mit Z bezeichnet, hinzu. Sie steht im rechten Winkel auf der X und der Y Achse. Die Z Achse bildet die dritte räumliche Dimension (siehe figure_projected_crs auf der rechten Seite). Jedem Punkt der mit Kugelkoordinaten dargestellt wird, kann eine X Y Z Koordinate zugeordnet werden.

Zwei- und dreidimensionale Koordinatenreferenzsysteme.

Ein projiziertes Koordinatenbezugssystem auf der Südhalbkugel (südlich des Äquators) hat nomalerweise seinen Ursprung an einem bestimmten Längengrad auf dem Äquator. Das bedeutet, dass die Y-Werte nach Süden und die X-Werte nach Westen anwachsen. Auf der Nordhalbkugel (nördlich des Äquators) liegt der Koordinatenursprung ebenfalls bei einem bestimmten Längengrad auf dem Äquator. Allerdings steigen die Y-Werte jetzt nordwärts und die X-Werte ostwärts an. Im folgenden Kapitel betrachte wir das projizierte Koordinatenbezugssystem Universal Transversal Mercator (UTM), das oft in Südafrika verwendet wird.

Das Universale Transversale Mercator (UTM) Koordinatensystem im Detail

Das Universale Transversale Mercator (UTM) Koordinatenbezugssystem hat seinen Ursprung auf dem Äquator an einem bestimmten Längengrad. Die Y-Werte steigen in Richtung Süd und die X-Werte in Richtung West an. Das UTM KBS ist eine globale Kartenprojektion. Das bedeutet, dass sie im allgemeinen weltweit verwendet wird. Wie bereits im Abschnitt ‚Genauigkeit von Kartenprojektionen‘ beschrieben, nimmt die Verzerrung von Winkeln, Abständen und Flächen mit der Größe des Gebietes zu (z.B. Südafrika). Um zu große Verzerrungen zu vermeiden, ist die Erde in 60 gleich große Zonen mit einer Breite von jeweils 6 Längengrad von Ost nach West geteilt. Wie in figure_utm_zones dargestellt, sind die UTM Zonen mit 1 bis 60 nummeriert, beginnend mit der internationalen Datumsgrenze (Zone 1 bei 180 Grad westlicher Länge) fortlaufend nach Osten bis zurück zur internationalen Datumsgrenze (Zone 60 bei 180 Grad östlicher Länge).

Die Universal Transveral Mercator Zonen. Für Südafrika werden die UTM Zonen 33S, 34S, 35S und 36S genutzt.

Wie man in den Abbildungen figure_utm_zones und figure_utm_for_sa sieht, wird Südafrika von vier UTM Zonen überdeckt, um Verzerrungen zu minimieren. Die Zonen sind bezeichnet mit UTM33S, UTM34S, UTM35S und UTM36S. Das S steht für die Lage der UTM Zonen südlich des Äquators.

UTM Zonen 33S, 34S, 35S und 36S mit ihren zentralen Längengraden (Meridianen), die zur hochgenauen Projektion für Südafrika verwendet werden. Das rote Kreuz zeigt ein Untersuchungsgebiet.

Wir wollen z.B. eine zweidimensionales Koordinate innerhalb des Untersuchungsgebietes, dass in der Abbildung figure_utm_for_sa mit einem roten Kreuz markiert ist, vergeben. Man sieht, dass das Gebiet innerhalb der UTM Zone 35S liegt. Wir sollten daher um Verzerrungen zu minimieren und genaue Analyseergebnisse zu erhalten das Koordinatenbezugssystem UTM zone 35S verwenden.

Die Position einer Koordinate in UTM südlich des Äquators enthält die Zonennummer (35), den Nordwert (Y) und den Ostwert (X) in Metern. Der Nordwert ist der Abstand der Position vom Äquator in Metern. Der Ostwert ist der Abstand vom Zentralmeridian (Längengrad) der verwendeten UTM Zone. Für die UTM Zone 35S sind es 27 Grad Ost wie in der Abbildung figure_utm_for_sa gezeigt. Da wir uns südlich des Äquators befinden und negative Werte im UTM Koordinatenbezugssystem nicht erlaubt sind, wird ein Offset für den Hochwert (Y) mit einem Wert von 10.000.000 m und ein Offset für den Rechtswert (X) mit einem Wert von 500.000 verwendet. Dies erscheint kompliziert, so dass wir ein Beispiel durchgehen, dass zeigt wie man die UTM 35S Koordinaten des Untersuchungsgebietes ermittelt.

Der Hochwert (Y)

Das Untersuchungsgebiet liegt 3.550.000 südlich des Äquators. Der Hochwert (Y) erhält daher ein negatives Vorzeichen: -3.550.000 m. Entsprechend der UTM Vorgabe müssen wir den Offset für den Hochwert in Höhe von 10.000.000 m dazu addieren. Das bedeutet, dass der Hochwert (Y) unserer Koordinate 6.450.000 m (-3.550.000 m + 10.000.000 m) beträgt.

Der Rechtswert (X)

Zuerst müssen wir den Zentralmeridian (Längengrad) der UTM Zone 35S identifizieren. Wie man in Abbildung figure_utm_for_sa sieht, liegt er bei 27 Grad Ost. Der Ort den wir suchen liegt 85.000 Meter westlich des Zentralmeridians. Genau wie der Hochwert erhält der Rechtswert (X) ein negatives Vorzeichen, wir erhalten -85.000 m als Ergebnis. Entsprechend der UTM Definition müssen wir einen Offset für den Rechtswert in Höhe von 500.000 m addieren. Damit ergibt sich für den Rechtswert (X) ein Koordinatenwert von 415.000 m (-85.000 m + 500.000 m). Zum Schluss muss noch die Zonennummer zum Rechtswert hinzugefügt werden, um den korrekten Wert zu erhalten.

Im Ergebnis lautet die Koordinate unseres Point of Interest projiziert im System UTM Zone 35S: 35 415.000 m O / 6.450.000 m N. In einigen GIS werden die Koordinaten einfach als 415.000 6.450.000 angezeigt, wenn die richtige UTM Zone 35S eingestellt ist und als Einheit Meter verwendet werden.

Spontane Reprojektion / On-The-Fly Projektion

Wie man sich wahrscheinlich denken kann, gibt es Situationen in denen die im GIS zu verwendenden Daten in verschiedenen Koordinatenbezugssystemen vorliegen. Man erhält z.B. einen Vektorlayer mit der Grenze Südafrikas im projizierten System UTM 35S und einen weiteren Vektorlayer mit Punktinformationen zum Niederschlag im geographischen Koordinatensystem WGS 84. Im GIS liegen diese zwei Vektorlayer in völlig verschiedenen Bereichen des Kartenfensters, da sie verschiedene Projektionen verwenden.

Um dieses Problem zu lösen besitzen viele GIS eine Funktion namens Spontane Kartenreprojektion („on-the-fly Projektion“). Das bedeutet, dass eine bestimmte Projektion beim Start des GIS definiert werden kann. Alle Layer, die in Folge geladen werden, werden ungeachtet dessen, welches Koordinatensystem dies selber aufweisen, automatisch in die Projektion umgerechnet, die zuvor definiert wurde. Diese Funktion erlaubt es, Layer in der Kartenansicht des GIS korrekt uberlappen zu lassen, selbst wenn diese unterschiedliche Koordinatenreferenzsysteme besitzen.

Bekannte Probleme / womit man rechnen muss

Die Thematik Kartenprojektion ist sehr komplex und selbst Profis die Geographie, Geodäsie oder eine andere GIS bezogene Wissenschaft studiert haben, haben oftmals Probleme mit der korrekten Definition der Kartenprojektion und des Koordinatenbezugssystems. In der Regel liegen für die Arbeit mit GIS bereits projizierte Daten vor. In den meisten Fällen werden diese Daten in ein bestimmtes KBS projiziert, so dass man in der Regel kein neues KBS anlegen oder die Daten in eine anderes KBS reprojizieren muss. Nichts desto trotz ist es sinnvoll, eine Vorstellung davon zu haben, was Kartenprojektion und KBS bedeuten.

Was haben wir gelernt?

Lassen Sie uns zusammenfassen, was wir in diesem Arbeitsblatt behandelt haben:

• Kartenprojektionen stellen die Erdoberfläche auf einem ebenen zweidimensionalen Papierstück oder Computerbildschirm dar.

• Es gibt Kartenprojektionen für die gesamte Erdoberfläche, aber die meisten Projektionen sind entworfen und optimiert, um kleinere Gebiete zu projizieren.

• Kartenprojektionen sind niemals eine völlig korrekte Repräsentation der kugelförmigen Erde. Sie zeigen Verzerrungen in Winkeln, Abständen und Flächen. Es ist in einer Kartenprojektion unmöglich, alle diese Eigenschaften gleichzeit zu erhalten.

• Ein Koordinatenbezugssystem (KBS) bestimmt mit Hilfe von Koordinaten, wie sich eine zweidimensionale projizierte Karte zu den tatsächlichen Orten auf der Erdoberfläche verhält.

• Es gibt zwei verschiedene Arten von Koordinatenbezugssystemen: geographische Koordinatensysteme und projizierte Koordinatensysteme.

• Die Projektion zur Laufzeit ist eine GIS-Funktionalität, die es uns erlaubt, Layer in verschiedenen projizierten Koordinatenbezugssystemen übereinander zu legen.

Versuchen Sie es selbst!

Hier sind einige Ideen für Sie, die Sie mit Ihren Lernenden versuchen sollten:

• Start QGIS and load two layers of the same area but with different projections and let your pupils find the coordinates of several places on the two layers. You can show them that it is not possible to overlay the two layers. Then define the coordinate reference system as Geographic/WGS 84 inside the Project Properties dialog and activate the checkbox Enable on-the-fly CRS transformation. Load the two layers of the same area again and let your pupils see how on-the-fly projection works.

• You can open the Project Properties dialog in QGIS and show your pupils the many different Coordinate Reference Systems so they get an idea of the complexity of this topic. With ‚on-the-fly‘ CRS transformation enabled you can select different CRS to display the same layer in different projections.

Etwas zum nachdenken

If you don’t have a computer available, you can show your pupils the principles of the three map projection families. Get a globe and paper and demonstrate how cylindrical, conical and planar projections work in general. With the help of a transparency sheet you can draw a two-dimensional coordinate reference system showing X axes and Y axes. Then, let your pupils define coordinates (X and Y values) for different places.

Literaturhinweise

Bücher:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986

• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195

• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

Webseiten:

• https://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html

• https://geology.isu.edu/wapi/geostac/Field_Exercise/topomaps/index.htm

Das QGIS Benutzerhandbuch beinhält mehr Informationen zum Arbeiten mit Kartenprojektionen in QGIS.

Wie geht es weiter?

Im folgenden Abschnitt werden wir uns das Thema Kartenproduktion näher ansehen.