Données Vecteurs¶

Vue d’ensemble¶

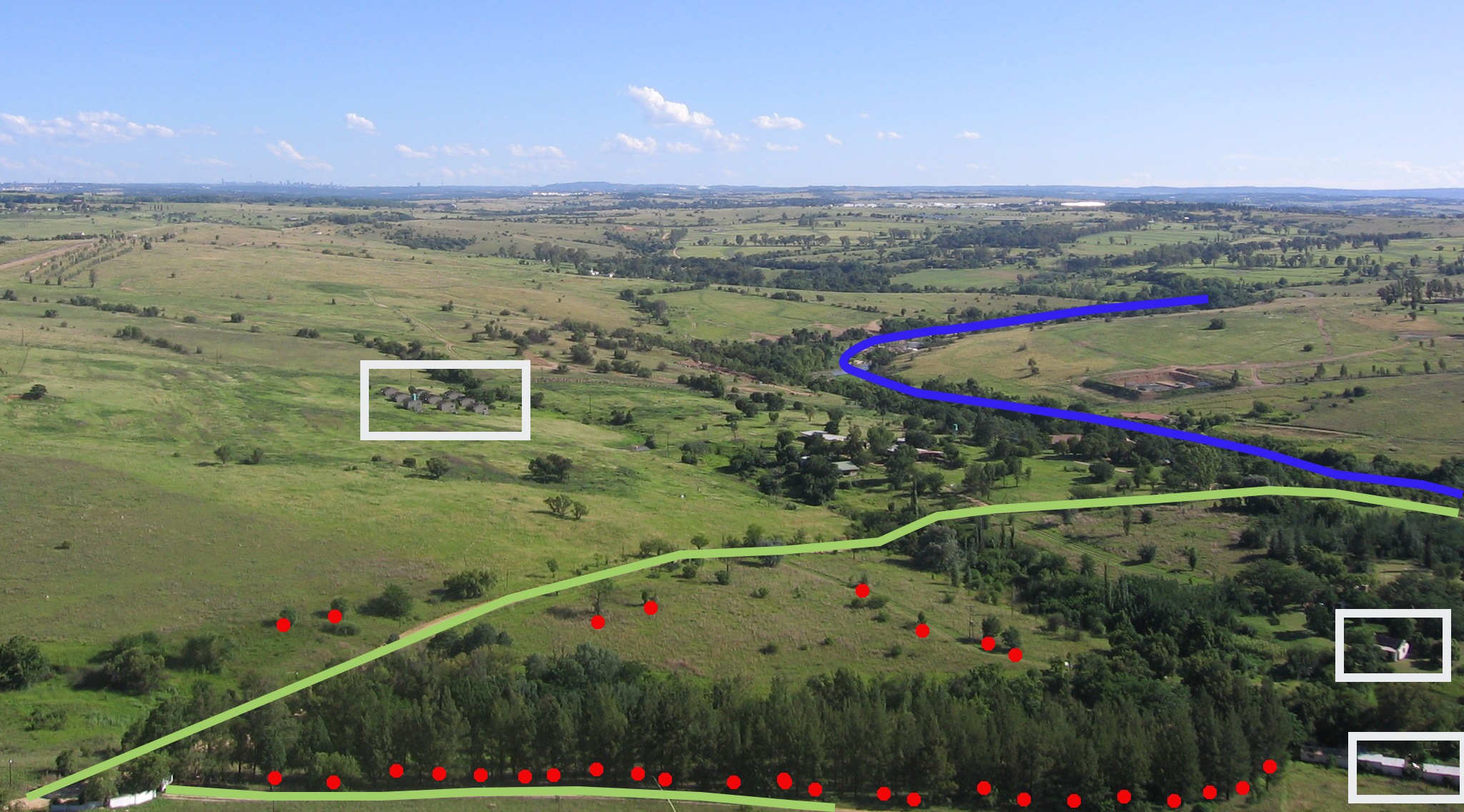
Les données Vecteurs fournissent un moyen de représenter le monde réel par des entités dans l’environnement SIG. Une entité est une chose que vous pouvez voir dans le paysage. Imaginez que vous êtes debout sur le sommet d’une colline. En regardant en bas, vous pouvez voir des maisons, des routes, des arbres, des rivières, et ainsi de suite (voir figure_landscape). Chacune de ces choses serait une entité quand nous les représentons dans une application SIG. Les données vecteurs ont des attributs, qui se composent d’informations texte ou numériques qui décrivent les entités.

Figure Landscape 1:

En regardant ce paysage, vous pouvez voir les entités principales, comme les routes, les maisons et les arbres.

Une entité vecteur a sa forme représentée en utilisant la géométrie. La géométrie est constituée d’un ou plusieurs sommets interconnectés. Un sommet décrit une position dans l’espace en utilisant un X, Y et éventuellement un axe Z. Les géométries qui ont des sommets avec un axe Z sont souvent désignés comme 2.5D car ils décrivent la hauteur ou la profondeur de chaque sommet, mais pas les deux.

Lorsque la géométrie d’une entité est composée d’un seul sommet, elle est référencée en tant qu’entité de point (consultez l’illustration figure_geometry_point). Lorsque la géométrie est composée d’un ou plusieurs sommets et que le premier et le dernier ne sont pas égaux, une entité de type polyligne est formée (illustration figure_geometry_polyline). Lorsque trois sommets ou plus sont présents et que le dernier sommet est égal au premier, une entité de polygone fermé est formée (illustration figure_geometry_polygon).

Figure Vector Geometries 1:

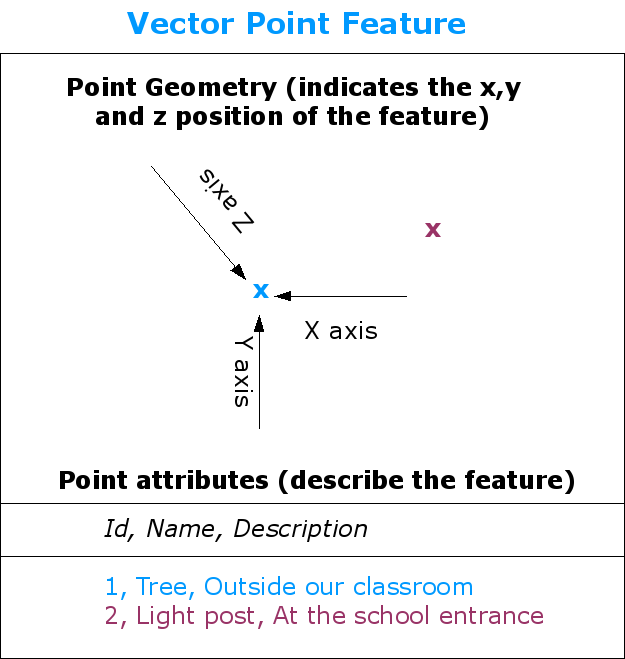
Une entité point est décrite par ses coordonnées X, Y et éventuellement Z. Les attributs du point décrivent le point, par exemple s’il s’agit d’un arbre ou d’un poteau de lampe.

Figure Vector Geometries 2:

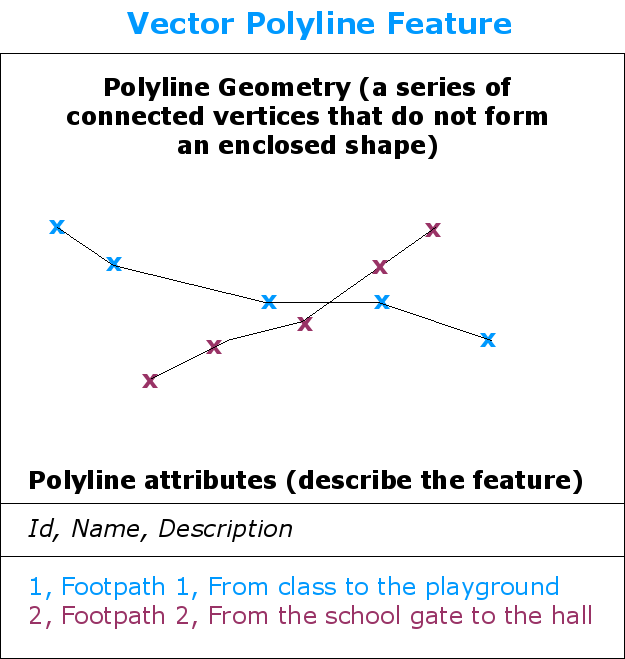
Une polyligne est une séquence de sommets reliés. Chaque sommet a des coordonnées X, Y (et éventuellement Z). Les attributs décrivent la polyligne.

Figure Vector Geometries 3:

Un polygone, comme une polyligne, est une séquence de sommets. Par contre dans un polygone, le premier et le dernier sommet sont toujours à la même position.

En regardant l’image du paysage que nous vous avons montré plus haut, vous devriez être capable de voir les différents types d’entités tel qu’un SIG les représente maintenant (voir illustration figure_geometry_landscape).

Figure Landscape 2:

Les entités du paysage tel que nous les représenterions dans un SIG. Les rivières (en bleu) et les routes (en vert) peuvent être représentées par des lignes, les arbres par des points (en rouge) et les maisons par des polygones (en blanc).

Une entité Point en détail¶

La première chose que nous devons réaliser en parlant des entités point est que ce que l’on décrit par un point en SIG est une question d’opinion, et cela dépend souvent de l’échelle. Regardons par exemple les villes. Si vous avez une petite échelle de carte (qui couvre une large surface), cela peut prendre sens de représenter une ville en utilisant une entité point. Par contre en zoomant sur la carte en allant vers une plus large échelle, cela prend plus de sens de montrer les limites des villes en tant que polygone.

Lorsque vous choisissez d’utiliser des points pour représenter une entité est surtout une question d’échelle (à quelle distance êtes-vous de l’entité), la commodité (cela prend moins de temps et d’efforts pour créer des points d’entités que des polygones), et le type d’entités (certaines choses comme les poteaux téléphoniques n’ont tout simplement pas de sens pour être stocké sous forme de polygones).

Comme nous l’avons montré dans l’illustration figure_geometry_point, une entité ponctuelle dispose de valeurs X,Y et optionnellement Z. Les valeurs X et Y dépendent du Système de Coordonnées de Référence (SCR) qui est utilisé. Nous allons étudier les Systèmes de Coordonnées de Référence plus en détail dans un prochain tutoriel. Pour le moment, disons simplement qu’un SCR est un moyen de décrire précisément l’emplacement d’un point à la surface de la Terre. L’un des systèmes de référence le plus courant est celui de la Longitude et Latitude. Les lignes de la Longitude vont du pôle Nord au pôle Sud. Les lignes de Latitude vont d’Est en Ouest. Vous pouvez décrire précisément où vous êtes sur la Terre en donnant votre longitude (X) et votre latitude (Y). Si vous faîtes la même chose pour un arbre ou un poteau téléphonique et que vous le marquez sur une carte, vous avez créé une entité de point.

Puisque nous savons la terre n’est pas plate, il est souvent utile d’ajouter une valeur Z pour une entité point. Ceci décrit à quel altitude au-dessus de niveau de la mer vous êtes.

Une entité Polyligne en détail¶

Là où une entité ponctuelle est un simple sommet, une polyligne en a deux ou plus. La polyligne est un chemin continu dessiné entre chaque sommet comme montré dans l’illustration figure_geometry_polyline. Lorsque deux sommets sont joints, une ligne est créée. Lorsque plus de deux sommets sont joints, ils forment une ‘ligne de lignes’ ou polyligne.

Une polyligne est utilisée pour montrer la géométrie des entités linéaires tels que les routes, les rivières, les contours, les sentiers, les trajectoires de vol et ainsi de suite. Parfois, nous avons des règles spéciales pour les polylignes en plus de leur géométrie de base. Par exemple les lignes de contour peuvent se toucher (par exemple à une falaise), mais ne doivent jamais s’entrecroiser. De même, des polylignes utilisées pour stocker un réseau routier doivent être raccordées à des intersections. Dans certaines applications de SIG, vous pouvez définir ces règles spéciales pour un type d’entités (par exemple, les routes) et le SIG veillera à ce que ces polylignes respectent toujours ces règles.

Si une polyligne courbe présente de grandes distances entre ses sommets, elle peut apparaître angulaire ou dentelée en fonction de l’échelle à laquelle elle est observée (voir figure_polyline_jagged). Il est donc important de numériser (capturer dans un ordinateur) les polylignes avec des distances entre sommets qui sont assez petites suivant l’échelle à laquelle vous souhaitez utiliser la donnée.

Figure Polyline 1:

Des polylignes vues à plus petite échelle (1:20 000 ou plus) peuvent apparaître lisses et incurvées. Lors d’un zoom pour une plus grande échelle (1:500 ou moins), les polylignes peuvent sembler très anguleux.

Les attributs d’une polyligne décrivent ses propriétés ou ses caractéristiques. Par exemple, une polyligne de route peut avoir des attributs qui décrivent si elle est recouverte de gravier ou de goudron, combien de voies il a, s’il s’agit d’une rue à sens unique, et ainsi de suite. Le SIG peut utiliser ces attributs pour symboliser l’entité polyligne avec une couleur ou le style de ligne approprié.

Une entité Polygone en détail¶

Les entités polygones sont des surfaces closes comme les barrages, les îles, les frontières des pays et ainsi de suite. Comme les entités polylignes, les polygones sont créés à partir d’une série de sommets qui sont reliés par une ligne continue. Toutefois, parce qu’un polygone décrit toujours un espace clos, les premiers et derniers sommets doivent toujours être au même endroit! Les polygones ont souvent une géométrie partagée — des limites qui sont en commun avec un polygone voisin. De nombreuses applications SIG ont la capacité de faire en sorte que les limites de polygones voisins coïncident exactement. Nous allons explorer cela dans le sujet Topologie plus loin dans ce tutoriel.

Comme avec des points et des polylignes, les polygones ont des attributs. Les attributs décrivent chaque polygone. Par exemple, un barrage peut avoir des attributs pour la profondeur et la qualité de l’eau.

Les données vecteurs dans les couches¶

Maintenant que nous avons décrit ce que sont les données vecteur, regardons comment les données de vecteur sont gérées et utilisées dans un environnement de SIG. La plupart des applications SIG regroupent les entités vecteur dans des couches. Les entités d’une couche ont le même type de géométrie (par exemple, ils seront tous points) et les mêmes types d’attributs (par exemple, l’information sur l’espèce d’un arbre au sein d’une couche arbres). Par exemple, si vous avez enregistré les positions de tous les sentiers dans votre école, ils seront généralement stockés ensemble sur le disque dur de l’ordinateur et affichés dans le SIG en une seule couche. C’est pratique car il vous permet de masquer ou d’afficher toutes les caractéristiques de cette couche dans votre application SIG avec un simple clic de souris.

Edition de données vecteurs¶

L’application SIG vous permettra de créer et de modifier les données de géométrie dans une couche — un processus appelé numérisation — que nous verrons de plus près dans un prochain tutoriel. Si une couche contient des polygones (par exemple les barrages agricoles), l’application SIG vous permettra de créer uniquement des nouveaux polygones dans cette couche. De même, si vous souhaitez modifier la forme d’une entité, l’application ne vous permet de le faire que si la forme modifiée est correcte. Par exemple, il ne vous permettra pas d’éditer une ligne de telle manière qu’il ne dispose que d’un sommet — souvenez-vous dans notre discussion sur les lignes ci-dessus que toutes les lignes doivent avoir au moins deux sommets.

La création et l’édition de données vecteur est une fonction importante d’un SIG, car il est l’un des principaux moyens par lesquels vous pouvez créer des données personnelles pour les choses qui vous intéressent. Par exemple, vous surveillez la pollution dans une rivière. Vous pouvez utiliser le SIG pour numériser tous les exutoires pour les drains d’eaux pluviales (comme des entités ponctuelles). Vous pouvez également numériser le fleuve lui-même (comme une entité polyligne). Enfin, vous pouvez prendre des mesures de niveaux de pH le long du cours de la rivière et de numériser les endroits où vous faites ces mesures (comme une couche de points).

Tout comme la création de vos propres données, il y a beaucoup de données vecteur que vous pouvez obtenir et utiliser de façon libre et gratuite. Par exemple, vous pouvez obtenir des données vectorielles apparaissant sur les feuillets cartographiques au 1:50 000 de la Direction générale: Études et levées cartographiques.

Échelle et données vecteur¶

L’échelle de la carte est un élément important lorsqu’on travaille avec des données vecteur dans un SIG. Lorsque la donnée est capturée, elle est généralement numérisée depuis des cartes existantes ou en récupérant l’information d’enregistrements terrain ou avec des périphériques GPS. Les cartes ont différentes échelles et si vous importez des données vecteur d’une carte dans un environnement SIG (par exemple en numérisant des cartes papier), la donnée vecteur aura les même problèmes d’échelle que la carte originelle. Cette effet peut être observé dans les illustrations figure_vector_small_scale et figure_vector_large_scale. De nombreux problèmes peuvent survenir d’un mauvais choix d’échelle de carte. Par exemple, utiliser les données vecteur de de l’illustration figure_vector_small_scale pour représenter les aires humides peut amener à ce que d’importantes surfaces de zones humides ne soient pas incluses dans la réserve ! D’un autre côté, essayer de créer une carte régionale en utilisant des données capturées au 1:1000 000 peut convenir et vous permettra d’économiser du temps et du travail de numérisation.

Figure Vector Scale 1:

Les données vecteur (lignes rouges) ont été numérisées à partir de cartes à petite échelle (1:1000 000).

Figure Vector Scale 2:

Les données vecteur (lignes vertes) ont été numérisées à partir de cartes à grande échelle (1:50 000)

Symbologie¶

Lorsque vous ajouter des couches vecteur dans la vue de carte d’une application SIG, elles seront dessinées avec des couleurs aléatoires et des symboles basiques. L’un des grands avantages d’utiliser un SIG est que vous pouvez personnaliser les cartes très facilement. Le programme de SIG vous laissera choisir les couleurs qui s’adapteront à votre type d’entité (ex: vous pouvez lui indiquer de dessiner les surfaces en eau en bleu). Le SIG vous permettra également d’ajuster les symboles utilisés. Si vous avez une couche ponctuelle d’arbres vous pouvez indiquer la position de chaque arbre avec une petite image d’abre plutôt qu’avec le cercle basique que le SIG a employé lors de l’ouverture initiale de la couche (voir les illustrations figure_vector_symbology, figure_generic_symbology et figure_custom_symbology).

Figure Vector Symbology 1:

Dans le SIG, vous pouvez utiliser un panneau (comme celui ci-dessus) pour régler comment les entités dans votre couche seront dessinées.

Figure Vector Symbology 2:

Lorsqu’une couche (par exemple la couche arbres ci-dessus) est chargée dans une application SIG pour la première fois, celle-ci lui attribuera un symbole par défaut.

Figure Vector Symbology 3:

Après nos réglages, il est plus facile de voir que nos points représentent des arbres.

La symbologie est une puissante fonctionnalité, donnant vie aux cartes et permettant la compréhension de vos données dans un SIG. Dans le sujet suivant (Attributs de données vectorielles) nous découvrirons plus en détail comment la symbologie peut aider l’utilisateur à comprendre la donnée vecteur.

Que faire avec une donnée vecteur dans un SIG?¶

Au niveau le plus simple, nous pouvons utiliser des données vectorielles dans une Application SIG de la même manière que vous utilisez une carte topographique normale. La réelle puissance des SIG commence à se manifester lorsque vous commencez à poser des questions telles que ‘quelles maisons sont dans le niveau de crue d’une rivière des 100 dernières années ?’ ; ‘où est la meilleure place pour mettre un hôpital qui soit facilement accessible à autant de personnes que possible ?’ ; ‘quels élèves vivent dans une banlieue particulière ?’. Un SIG est un bon outil pour répondre à ces types de questions avec l’aide des données vectorielles. Nous faisons généralement allusion à l’analyse spatiale pour le processus de réponse à ces types de questions. Dans les sujets suivants de ce tutoriel, nous regarderons plus en détail l’analyse spatiale.

Problèmes courants avec les données vecteur¶

Travailler avec des données vecteur n’est pas sans soulever de problèmes. Nous avons déjà mentionné les problèmes qui surviennent avec les vecteurs capturés à différentes échelles. Les données vecteur nécessitent également beaucoup d’effort et de maintenance pour s’assurer qu’elles sont précises et fiables. Des données vecteur imprécises peuvent être capturées par des instruments qui ne sont pas configurés correctement ou bien lorsque les personnes qui enregistrent les données ne sont pas assez attentives, lorsque le temps ou l’argent ne suffisent pas à collecter suffisamment de détails, etc.

Si vous avez des données vecteur de faible qualité, vous pouvez souvent les détecter lorsque vous visualiser ces données dans un SIG. Par exemple, des écarts peuvent apparaître lorsque les segments de deux polygones ne se rencontrent pas correctement (voir figure_vector_slivers).

Figure Vector Issues 1:

Les écarts proviennent du non-alignement des limites de deux polygones adjacents. A une petite échelle (ex: 1 à gauche), ces erreurs ne sont pas visibles. A une grande échelle, elles sont visibles sous la forme de fines bandes entre les deux polygones (2 à droite).

Les croisements apparaissent lorsqu’une entité linéaire telle qu’une route ne rencontre pas une autre route au niveau de l’intersection. Les non-connexions apparaîssent lorsqu’une entité linéaire (ex: une rivière) ne rencontre pas exactement une autre entité avec laquelle est devrait être connectée. L’image figure_vector_overshoots montre un exemple de croisement et de non-connexion.

Figure Vector Issues 2:

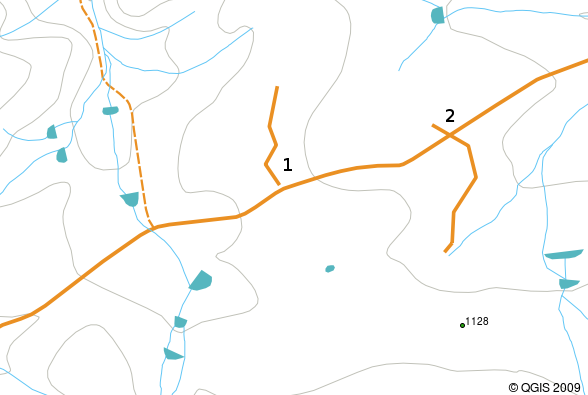
Des non-connexions (1) se produisent lorsque des lignes vectorielles numérisées qui doivent se connecter les unes aux autres ne se touchent pas. Des croisements (2) apparaissent si une ligne se termine au-delà de la ligne avec laquelle elle doit être connectée.

Pour éviter ce genre d’erreur, il est important de numériser la donnée en faisant attention et en étant précis. Dans le chapitre à venir sur la topologie nous étudierons quelques-unes de ces erreurs en détails.

Qu’avons-nous appris?¶

Faisons le point sur ce que nous avons abordé dans cette partie:

• La donnée vecteur est utilisée pour représenter les entités du monde réel dans un SIG.

• Une entité vectorielle peut avoir une géométrie de type point, polyligne ou polygone.

• Chaque entité vecteur a des données attributaires qui la décrivent.

• La géométrie de l’entité est décrite en termes de sommets.

• Les géométries de type Point sont composées de sommet unique (coordonnées X,Y et éventuellement Z).

• Les géométries de type Polyligne sont composées de deux ou plusieurs sommets reliés en ligne.

• Les géométries de type Polygone sont construites avec au moins quatre sommets formant une surface close. Les premier et dernier sommets sont toujours au même endroit.

• Le choix du type de géométrie dépend de l’échelle, de sa commodité et de ce que vous voulez faire avec les données dans le SIG.

• La plupart des applications SIG ne vous permettent pas de mélanger plus d’un type de géométrie dans une même couche.

• La numérisation est le processus de création de données vecteur, en les dessinant au sein d’une application SIG.

• Les données vecteurs peuvent présenter des problèmes de qualité comme les croisements, les non-connexions et les écarts dont vous devez connaître l’existence.

• Les données vecteur peuvent être utilisées pour des **analyses spatiales dans une application SIG, par exemple pour trouver l’hôpital le plus proche d’une école.

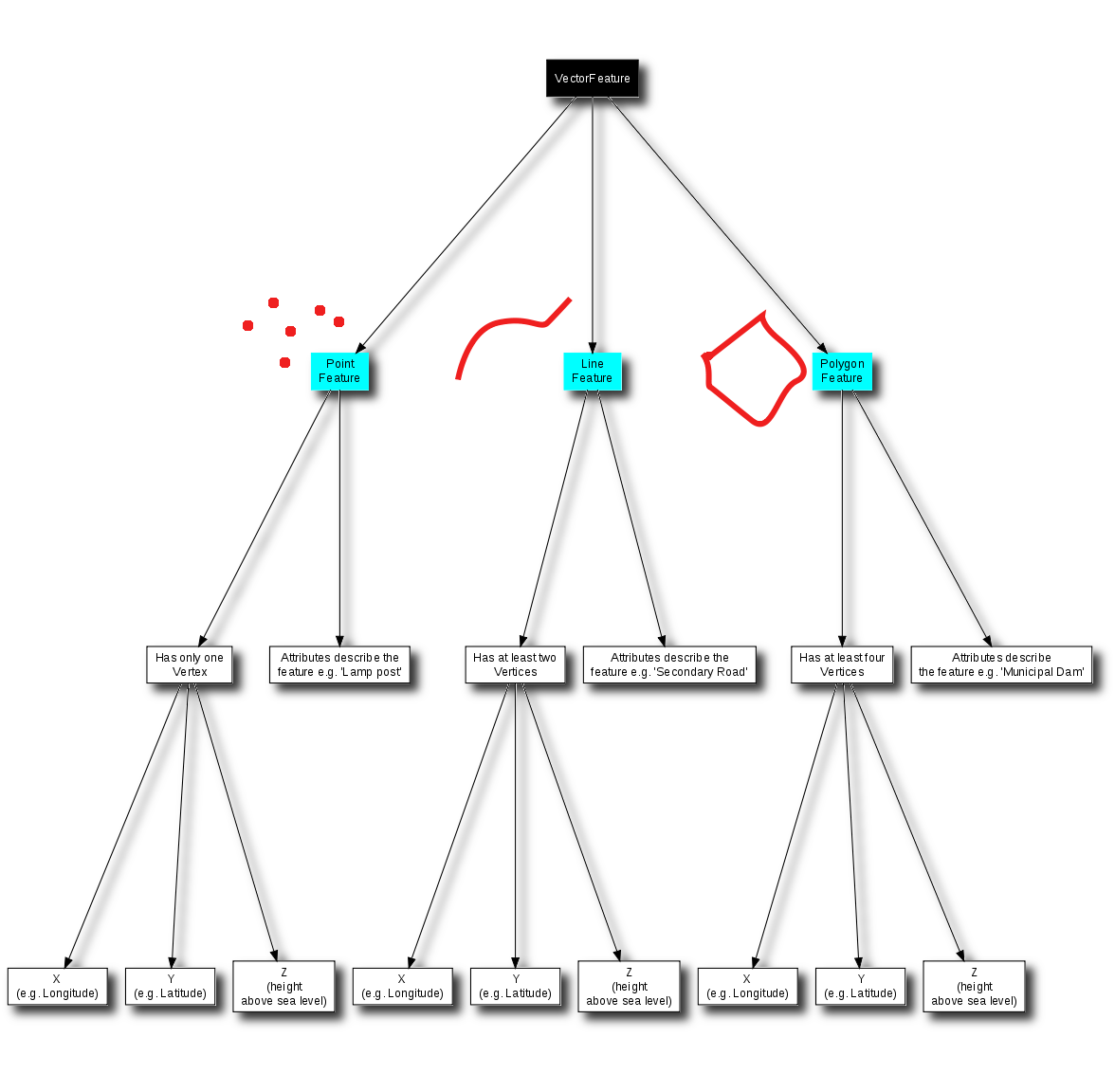
Nous avons résumé le concept de données vecteur en SIG dans la figure figure_vector_summary.

Figure Vector Summary 1:

Ce diagramme montre comment les applications SIG gèrent les données vecteur.

Maintenant, essayez !¶

Voici quelques pistes d’actions à essayer avec vos élèves:

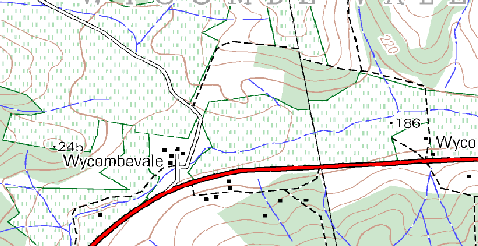
• Sur une copie de carte topographique d’un lieu près de chez vous (comme celui sur la figure_sample_map), demandez à vos élèves de retrouver et surligner des exemples de différents types de données vecteur.

• Réfléchissez à comment vous créeriez des entités vecteurs dans un SIG pour représenter les objets du monde réel que constitue votre cour d’école. Créez une table des différentes entités dans et autour de l’école et demandez ensuite aux élèves de décider si ces entités seraient mieux représentées dans un SIG par un point, une ligne ou un polygone. La table_vector_1 constitue un exemple.

Figure Sample Map 1:

Pouvez-vous identifier deux entités Point et une entité Polygone sur cette carte?

Table vecteur 1: Créez une table comme celle-ci (en laissant la colonne géométrique vide) et demandez à vos élèves de choisir les types géométriques adaptés.

A retenir¶

Si vous n’avez pas d’ordinateur à disposition, vous pouvez utiliser une carte topographique et du papier calque pour présenter les données vecteurs à des élèves.

Pour aller plus loin¶

Le Guide de l’Utilisateur de QGIS fournit aussi des informations plus détaillées sur l’utilisation de données vecteur dans QGIS.

La suite ?¶

Dans la section qui suit nous aborderons les données attributaires pour voir comment elles peuvent être utilisées pour décrire les entités vecteur.